Очень У меня 1.5 часа. Хотя бы одно задание, только полностью

Пошаговое объяснение:

1, Средняя скорость 80 км/час., Настя добиралась до работы больше одного часа, следовательно ехала с меньшей скоростью, чем средняя. Поэтому она не могла ехать со средней  коростью сто км/час.

2. Скорость внука х км/час

средняя скорость деда и отца одинакова, т.к. оба половину дороги пробежали со скоростью в два раза меньше, чем скорость сына(внука),а полдороги со скоростью в три раза больше, чем скорость мальчика. Поэтому они вернутся домой одновременно.

Теперь расчитаем время затраченное на дорогу,

внук:   S/х

средняя скорость на дорогу в оба конца отца и деда:

(0,5х+3х):2=3,5х:2=1,75х

время затраченное отцом и дедом:

S/1,75х

отец и дед вернутся раньше.

или

Пошаговое объяснение:

Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).

Решать задачу будем следующим образом:

 вспомним формулу для нахождения расстояния между точками на плоскости;

 обозначим точки равноудаленные от А и В координатами (x; y);

 запишем расстояния между точкой А и (x; y);

 запишем расстояние между точками B и (x; y);

 приравняем расстояния и выразим одну переменную через другую.

Вспомним формулу для нахождения расстояния на плоскости

Формула для нахождения расстояния между точками на плоскости выглядит так:

AB =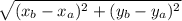 , где точки А и В заданы координатами A  и B

Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).

Составим уравнение геометрического места точек

Записываем расстояние между точкой A (2; -3) и (x; y):

;

Записываем расстояние между точками B (-4; 1) и (x; y):

;

Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:

;

;

Открываем скобки, переносим все слагаемые в право и приводим подобные.

;

или  

.