Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго периода вычесть число, стоящее до первого периода, результат записать в числителе; в знаменатель записать число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между запятой и периодом.
1) 2,1(6)- в числителе ставим 16-1, знаменателе ставим 90, т.к. до периода 1 цифра ее меняем на 9 и в периоде 1 цифра ее меняем на 0, получим
=2 (16-1)/90=2 15/90=2 1/6
2) 5,14(33)= здесь в числителе будет 1433-14, а в знаменателе 9900
Пусть число а,b(c) периодичное, где а - целая часть, b - число в предпериоде, c - число в периоде, в нашем примере а=2, b=1, c=6. Чтобы преобразовать эту дробь в обыкновенную нужно придерживаться следующему правилу:
а) Считаем количество цифр в периоде десятичной дроби и обозначаем количество цифр через k, в нашем примере k=1, так как число 6 состоит из одной цифры;
б) Считаем количество цифр, стоящих в предпериоде, то есть количество цифр, стоящих после запятой, но до периода десятичной дроби и обозначаем количество цифр через m, в нашем примере m=1, так как число 1 состоит из одной цифры;
в) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа , в нашем примере n=16;
г) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа , в нашем примере s=1;
д) Подставляем найденные значения в формулу
Нетрудно видеть, что состоит из k цифр 9, а из m цифр 0 после 1.
В нашем примере
2) 5,14(33) ⇒ a=5, k=2, m=2, n=1433, s=14. Тогда
3) 0,11(35) ⇒ a=0, k=2, m=2, n=1135, s=11. Тогда
4) 0,214(45) ⇒ a=0, k=2, m=3, n=21445, s=214. Тогда
Пошаговое объяснение:
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго периода вычесть число, стоящее до первого периода, результат записать в числителе; в знаменатель записать число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между запятой и периодом.
1) 2,1(6)- в числителе ставим 16-1, знаменателе ставим 90, т.к. до периода 1 цифра ее меняем на 9 и в периоде 1 цифра ее меняем на 0, получим
=2 (16-1)/90=2 15/90=2 1/6
2) 5,14(33)= здесь в числителе будет 1433-14, а в знаменателе 9900
5 (1433-14)/9900= 5 1419/9900=5 43/300
3) 0,11(35)= числитель 1135-11, знаменатель 9900
(1135-11)/9900=1124/9900=281/2475
4) 0,214(45)=числитель 21445-214, знаменатель 99000
(21445-214)/99000=21231/99000=2359/11000
Пошаговое объяснение:
Общую схему рассмотрим в примере 1) 2,1(6).
Пусть число а,b(c) периодичное, где а - целая часть, b - число в предпериоде, c - число в периоде, в нашем примере а=2, b=1, c=6. Чтобы преобразовать эту дробь в обыкновенную нужно придерживаться следующему правилу:
а) Считаем количество цифр в периоде десятичной дроби и обозначаем количество цифр через k, в нашем примере k=1, так как число 6 состоит из одной цифры;
б) Считаем количество цифр, стоящих в предпериоде, то есть количество цифр, стоящих после запятой, но до периода десятичной дроби и обозначаем количество цифр через m, в нашем примере m=1, так как число 1 состоит из одной цифры;
в) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа , в нашем примере n=16;
г) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа , в нашем примере s=1;
д) Подставляем найденные значения в формулу
Нетрудно видеть, что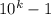
состоит из k цифр 9, а 
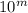из m цифр 0 после 1.
В нашем примере
2) 5,14(33) ⇒ a=5, k=2, m=2, n=1433, s=14. Тогда
3) 0,11(35) ⇒ a=0, k=2, m=2, n=1135, s=11. Тогда
4) 0,214(45) ⇒ a=0, k=2, m=3, n=21445, s=214. Тогда