и стоимость не может быть отрицательной x - 5 >= 0 x - 24 >= 0 и x - 28 >= 0
общее x >= 28
решаем неравенство
3х - 57 < x
2x < 57
x < 28,5
если считать, что стоимость батона целое число , то он стоит 28 рублей(если нет то от 28 до 28.5 рублей)
ну и можно рассуждениями, считая что стоимость батона целая
Маше не хватало 5 рублей, когда сложили, то снова не хватило. получается, что у Насти и Милы не было 5 рублей, чтобы одолжить , а было 4. у Милы денег не было, у Насти было 4 рубля и у Маши 23 рубля.
Рассмотрим все возможные непустые наборы, состоящие из каких-то из 10 выбранных чисел. Таких наборов 1023: каждое число можно независимо взять или не взять в набор, это даст вариантов, и 1 вариант, когда набор пустой, нужно исключить.
Выпишем сумму чисел каждого из таких наборов. Максимальное возможное выписанное значение , так что различных возможных сумм не больше 955. Поскольку мы выписали 1023 суммы, значит, какие-то два набора имеют одинаковую сумму.
Из каждого из найденных наборов исключим числа, входящие в оба набора (если такие числа есть, конечно). Суммы чисел останутся равными, поскольку обе суммы уменьшились на одно и то же число; получившиеся наборы будут непусты (ни один набор не может полностью входить в другой, иначе их суммы были бы не равны).
Итак, мы получили, что нашлись два набора, содержащие разные числа, имеющие одинаковые суммы. Ура!
можно решать через переменную
пусть х - стоимость батона
тогда у Маши х - 5
у Насти х - 24
у Милы х - 28
х - 28 + х - 24 + х - 5 < x
и стоимость не может быть отрицательной x - 5 >= 0 x - 24 >= 0 и x - 28 >= 0
общее x >= 28
решаем неравенство
3х - 57 < x
2x < 57
x < 28,5
если считать, что стоимость батона целое число , то он стоит 28 рублей(если нет то от 28 до 28.5 рублей)
ну и можно рассуждениями, считая что стоимость батона целая
Маше не хватало 5 рублей, когда сложили, то снова не хватило. получается, что у Насти и Милы не было 5 рублей, чтобы одолжить , а было 4. у Милы денег не было, у Насти было 4 рубля и у Маши 23 рубля.
Рассмотрим все возможные непустые наборы, состоящие из каких-то из 10 выбранных чисел. Таких наборов 1023: каждое число можно независимо взять или не взять в набор, это даст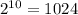 вариантов, и 1 вариант, когда набор пустой, нужно исключить.
вариантов, и 1 вариант, когда набор пустой, нужно исключить.
Выпишем сумму чисел каждого из таких наборов. Максимальное возможное выписанное значение , так что различных возможных сумм не больше 955. Поскольку мы выписали 1023 суммы, значит, какие-то два набора имеют одинаковую сумму.
, так что различных возможных сумм не больше 955. Поскольку мы выписали 1023 суммы, значит, какие-то два набора имеют одинаковую сумму.
Из каждого из найденных наборов исключим числа, входящие в оба набора (если такие числа есть, конечно). Суммы чисел останутся равными, поскольку обе суммы уменьшились на одно и то же число; получившиеся наборы будут непусты (ни один набор не может полностью входить в другой, иначе их суммы были бы не равны).
Итак, мы получили, что нашлись два набора, содержащие разные числа, имеющие одинаковые суммы. Ура!