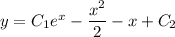Пусть , получим:
Умножим левую и правую части уравнения на множитель :
, получаем
Интегрируя обе части уравнения, получим
Выполним обратную замену:
ответ:
Пусть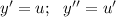 , получим:
, получим:
Умножим левую и правую части уравнения на множитель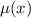 :
:
Интегрируя обе части уравнения, получим
Выполним обратную замену:
ответ: