ответ:
Пошаговое объяснение:
Данное диф. уравнение является уравнением с разделяющимися переменными.... Разделим же переменные и затем проинтегрируем обе части уравнения
Найдем теперь частное решение, подставляя начальные условия
— частное решение.
ответ: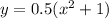
Пошаговое объяснение:
Данное диф. уравнение является уравнением с разделяющимися переменными.... Разделим же переменные и затем проинтегрируем обе части уравнения
Найдем теперь частное решение, подставляя начальные условия