Пусть какое-либо из искомых четырехзначных чисел имеет вид . Тогда, после применения указанной операции, будет получено число , кратное 14.
Очевидно, .
Проверим делимость второго множителя на 7:
То есть делится на 7. Но, очевидно, на 2 не делится (т.к. нечетно). Значит, для делимости на 14=2*7 числа необходимо и достаточно, чтобы делилось на 2.
То есть искомое множество чисел - все четные четырехзначные числа.
Все четные четырехзначные числа
Пошаговое объяснение:
Пусть какое-либо из искомых четырехзначных чисел имеет вид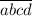 . Тогда, после применения указанной операции, будет получено число
. Тогда, после применения указанной операции, будет получено число 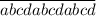 , кратное 14.
, кратное 14.
Очевидно,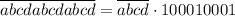 .
.
Проверим делимость второго множителя на 7:
То есть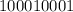 делится на 7. Но, очевидно, на 2 не делится (т.к. нечетно). Значит, для делимости на 14=2*7 числа
делится на 7. Но, очевидно, на 2 не делится (т.к. нечетно). Значит, для делимости на 14=2*7 числа 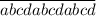 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 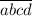 делилось на 2.
делилось на 2.
То есть искомое множество чисел - все четные четырехзначные числа.