Здесь должно быть целым натуральным и введём откуда , где .
В дробь подставим и найдём для какого наименьшего целого положительного k число натуральное.
Откуда получаем при наименьшем . Следовательно искомое натуральное число
ответ: 2034142.
Здесь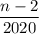 должно быть целым натуральным и введём
должно быть целым натуральным и введём 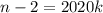 откуда
откуда 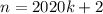 , где
, где 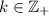 .
.
В дробь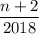 подставим
подставим 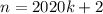 и найдём для какого наименьшего целого положительного k число натуральное.
и найдём для какого наименьшего целого положительного k число натуральное.
Откуда получаем при наименьшем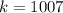 . Следовательно искомое натуральное число
. Следовательно искомое натуральное число 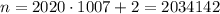
ответ: 2034142.