в) [4; +∞)
Пошаговое объяснение:
Каждое из слагаемых положительное. При sin x=0 или cos x=0 получаем +∞, это верхняя грань. Если , то это нижняя грань.
.
Нижняя грань достигается и при значениях .
Значит область значений E(y)=[4;+∞).
в) [4; +∞)
Пошаговое объяснение:
Каждое из слагаемых положительное. При sin x=0 или cos x=0 получаем +∞, это верхняя грань. Если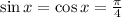
, то это нижняя грань.
Нижняя грань достигается и при значениях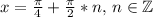
.
Значит область значений E(y)=[4;+∞).