Задание по математике ,поэтому в физику не углубляемся.
Перед отправкой (то есть, когда скорость тепловоза была равна 0) частота гудка была равна f(0)=440 Гц.
Из-за эффекта Доплера частота гудка становится больше, зависит это от скорости тепловоза.
По условию,частота гудка может отличаться не более,чем на 10 Гц (иначе,человек не услышит гудок).
Нам надо найти скорость,с которой тепловоз должен приближаться к платформе,если человек смог различать сигнал тепловоза.
Рассчитывается по формуле,данной ниже (далее идут просто расчёты).
Подставляем все известные данные в формулу и находим минимальную скорость тепловоза.
.
Разделим предварительно х²+5 на (х+1), ПОЛУЧИМ х-1 И В ОСТАТКЕ 6
х²+5 ⊥(х+1)
-(х²+х) (Х-1)
-х+5
-(х+1)
6
представим теперь дробь (х²+5)/(х+1) в виде (х-1)+(6/(х+1)), взяв затем интеграл от каждого из слагаемых отдельно. получим табличные интегралы.
х²/2-х+6㏑Ix+1I
Воспользуемся формулой Ньютона -Лейбница, подставив сначала верхний, потом нижний интеграл, вычитая от первого второй, получим
1²/2-1+6㏑I1+1I - ( 0²/2-0+6㏑I0+1I)=0.5-6㏑2, т.к. ㏑1=0; ответ можно записать и так 0.5-㏑2⁶=0.5-㏑64
Задание по математике ,поэтому в физику не углубляемся.
Перед отправкой (то есть, когда скорость тепловоза была равна 0) частота гудка была равна f(0)=440 Гц.
Из-за эффекта Доплера частота гудка становится больше, зависит это от скорости тепловоза.
По условию,частота гудка может отличаться не более,чем на 10 Гц (иначе,человек не услышит гудок).
Нам надо найти скорость,с которой тепловоз должен приближаться к платформе,если человек смог различать сигнал тепловоза.
Рассчитывается по формуле,данной ниже (далее идут просто расчёты).
Подставляем все известные данные в формулу и находим минимальную скорость тепловоза.
.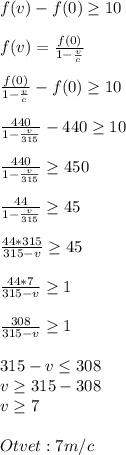
Разделим предварительно х²+5 на (х+1), ПОЛУЧИМ х-1 И В ОСТАТКЕ 6
х²+5 ⊥(х+1)
-(х²+х) (Х-1)
-х+5
-(х+1)
6
представим теперь дробь (х²+5)/(х+1) в виде (х-1)+(6/(х+1)), взяв затем интеграл от каждого из слагаемых отдельно. получим табличные интегралы.
х²/2-х+6㏑Ix+1I
Воспользуемся формулой Ньютона -Лейбница, подставив сначала верхний, потом нижний интеграл, вычитая от первого второй, получим
1²/2-1+6㏑I1+1I - ( 0²/2-0+6㏑I0+1I)=0.5-6㏑2, т.к. ㏑1=0; ответ можно записать и так 0.5-㏑2⁶=0.5-㏑64