Найдите косинус угла С треугольника АВС , если
А (0,1,-1) , В (1,-1,2) , С (3,1,0)
Вариант II.
1 Даны точки А (3,2,1), В (1,2,3) и вектор CD (1,1,1).
Найдите:
а) координаты вектора АВ;
б) абсолютную величину вектора CD ;
в) координаты разности векторов АВ и CD ;
2 Найдите длину вектора 2 ⃗ + 3 ⃗ , если
координаты векторов ⃗ (1,1,-1) , ⃗ (2,0,0);
3 Найдите косинус угла В треугольника АВС , если
А (2,2,-4), В (2,-1,-1) , С (3,-1,-2)

Показать ответ

Ответ:

vikylyalol

25.06.2020 17:15

Угол между осями координат 90°, поэтому треугольник получиться прямоугольным. Найти площадь круга можно через радиус, а радиус, описанной окружности около прямоугольного треугольника, можно найти через его гипотенузы (половина от гип.) т.к. угол в 90° опирается на диаметр, то есть гипотенуза это диаметр. Так вот нам надо найти гипотенузы этого треугольника, а именно её половину. Для этого найдём точки пересечения прямой с осями координат, а затем расстояние между ними, это и будет гипотенуза, дальше думаю понятно.

0,0(0 оценок)

Ответ:

1652001

03.02.2020 15:36

$v=\frac{1}{3} *\frac{1}{2} *15*15\sqrt{3}*\frac{1}{2} *\sqrt{15^{2} + (15\sqrt{3})^{2} } /(2\sqrt{3} / 225 )$

Пошаговое объяснение:

ДАНО: ПИРАМИДА

ΔАВС- прямоугольный

АВ=15, ВС=15√3

∠a =arctg(2√3)/225

НАЙТИ: Vпирамиды

V= 1/3 Sосн*h

1) ΔABC прямоугольный AB, BC катеты, Sосн=1/2*AB*BC

2) Высота пирамиды "h", опущенная из вершины D, в точку "0", причем "0" является точкой центром описанной окружности ΔАВС, то есть, точкой пересечения срединных перпендикуляров, проведенных к сторонам ΔАВС.(в часном случае ΔАВС прямоугольный, и "О" лежит на гипотенузе АС )

Δ ΔОЕВ - прямоугольный , с катетами "ОЕ" "ОМ" и дпины их равны половине соответствующих катетов ΔАВС OB²=OE²+OM²=1/4(AB²+BC²)

Из ΔDBO Прямоугольный, известен катет и прилежащий угол,

∠a нам дан. tg∠a= OE/OB OE=OB/tg∠a

рабочая формула будет иметь вид

V=1/3 *1/2*AB*BC* h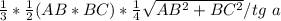 $\frac{1}{3} *\frac{1}{2} (AB*BC)*\frac{1}{4}\sqrt{AB^{2}+BC^{2} } /tg\ a$