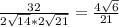Пошаговое объяснение:
Чтобы найти косинус угла между векторами нужно, скалярное произведение этих векторов разделить на произведение их длин.
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = (-2) · 4 + 4 · (-2) + 6 · 8 = -8 - 8 + 48 = 32
Найдем длины векторов:
|a| = √ax2 + ay2 + az2 = √(-2)2 + 42 + 62 = √4 + 16 + 36 = √56 = 2√14
|b| = √bx2 + by2 + bz2 = √42 + (-2)2 + 82 = √16 + 4 + 64 = √84 = 2√21
Найдем угол между векторами:
cosα =
Пошаговое объяснение:
Чтобы найти косинус угла между векторами нужно, скалярное произведение этих векторов разделить на произведение их длин.
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = (-2) · 4 + 4 · (-2) + 6 · 8 = -8 - 8 + 48 = 32
Найдем длины векторов:
|a| = √ax2 + ay2 + az2 = √(-2)2 + 42 + 62 = √4 + 16 + 36 = √56 = 2√14
|b| = √bx2 + by2 + bz2 = √42 + (-2)2 + 82 = √16 + 4 + 64 = √84 = 2√21
Найдем угол между векторами:
cosα =