Формула площади трапеции через стороны (вывод ниже):
Объем прямой призмы равен произведению площади основания S на высоту призмы h:
ответ: Объем призмы равен 3690 см³.
_______________________________
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y. Таким образом x+y = d−b, y = d−b−x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем:
a²−x² = c²−y² или x²−y² = a²−c².
Подставляем вместо х полученное выше выражение d−b−x:
x²−(d−b−x)² = a²−c²
x²−d²+bd+dx-b²+bd−bx−x²+dx−bx = a²−c²
x²−d²+2bd+2dx−b²−2bx−x² = a²−c²
2dx−2bx = a²−c²+d²+b²−2bd
2x(d−b)=a²−c²+(d−b)²
Подставляем обратно x в формулу высоты:
Формула площади трапеции через стороны будет выглядеть так:
Пошаговое объяснение:
a)
-2*(x - 1)+3x = 7
-2x + 2 + 3x = 7
x + 2 = 7
x = 7 - 2
x = 5
-2*(5 - 1) + 3*5 = 7
-2*4 + 15 = 7
-8 + 15 = 7
7 = 7
б)
5y - (3 - y) + (2y - 1) = y + 3
5y - 3 + y + 2y - 1 = y + 3
8y - 4 = y + 3
8y - y = 3 + 4
7y = 7
y = 7:7
y = 1
5*1 - (3 - 1) + (2*1 - 1) = 1 + 3
5 - 2 + 1 = 4
4 = 4
2*(x - 5) - 3*(x + 4) = x - 22
2x - 10 - 3x - 12 = x - 22
-x - 22 = x - 22
x + x = -22 + 22
2x = 0
x = 0
a)
-3*(x - 2) + 4x = 11
-3x + 6 + 4x = 11
x + 6 = 11
x = 11 - 6
x = 5
-3*(5 - 2) + 4*5 = 11
-3*3 + 20 = 11
-9 + 20 = 11
11 = 11
б)
2y - (4 - y) + (3y - 2) = y + 4
2y - 4 + y + 3y - 2 = y + 4
6y - 6 = y + 4
6y - y = 4 + 6
5y = 10
y = 10 : 5
y = 2
2*2- (4 - 2) + (3*2 - 2) = 2 + 4
4 - 2 + 4 = 6
6 = 6
3 *(x - 4) - 4*(x + 5) = -30 + x
3x - 12 - 4x - 20 = -30 + x
-x - 32 = -30 + x
x + x = -32 + 30
2x = -2
x = -2 : 2
x = -1
Формула площади трапеции через стороны (вывод ниже):
Объем прямой призмы равен произведению площади основания S на высоту призмы h:
ответ: Объем призмы равен 3690 см³.
_______________________________
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y. Таким образом x+y = d−b, y = d−b−x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту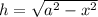
и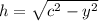 
. Приравнивая, получаем:
a²−x² = c²−y² или x²−y² = a²−c².
Подставляем вместо х полученное выше выражение d−b−x:
x²−(d−b−x)² = a²−c²
x²−d²+bd+dx-b²+bd−bx−x²+dx−bx = a²−c²
x²−d²+2bd+2dx−b²−2bx−x² = a²−c²
2dx−2bx = a²−c²+d²+b²−2bd
2x(d−b)=a²−c²+(d−b)²
Подставляем обратно x в формулу высоты:
Формула площади трапеции через стороны будет выглядеть так: