На юге или на севере?
линия 1: (-4; 2) (-3; 4) (0; -6) (1; 4) (2; 5) (3; -5) (6; —7) (4; —8) (2; —8)
(2; -9) (6; -9) (8; -8) (8; 4) (9; -6) (14; 4) (14; 0) (11; 2) (8; 1) (2; 1) (-1; 2)
(-4; -2)
линия 2: (-4; — 2) (-8; —3) (-11; -5) (-12; —8) (-15; -9) (-16; —10) (-12; —9)
(-11; -11) (-12; —14) (-9; —14) (-9; —13) (-8; —13) (-9; —10) 9–3; -10) (-3; —15) (0; —15) (0; —11) (1; -11) (1; —
12) (0; —14) (2; —15) (4; —12) (4; -9)
поставь точки: (4; —2) и (7; -2)
Такое надо в уме решать...в идеале..
на числовой прямой отмечаем нули функции, т.е точки при значении которых каждый двучлен равен 0.
Отмечаем закрашенную точку 4, и выколотую -1, т.к. знаменатель неравен 0.
Дальше рассматриваете интервалы:
От -∞ до -1 не включая, оба выражения отрицательны, а значит, само выражение положительно. Ставим +.
От -1 до 4, нижнее строго больше нуля, верхнее меньше или равно нулю. Все выражение меньше или равно нулю. Ставим -.
От 4 до +∞, и нижнее, и верхнее больше нуля, значит, ставим +.
Смотрим, нам подходит только средний интервал, т.е. х принадлежит от -1 до 4 вкл.
ответ: х∈(-1; 4].
Задачка довольно не простая, поэтому решение будет длинным.
Просто хочу сказать что все что я решал до этого привело меня в полное безумие. И этим решением является текст данный мной ниже.
Так как гипотенуза равна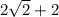 и один из катетов например AC = x, то катет AB =
и один из катетов например AC = x, то катет AB = 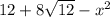
Проводим биссектрисы из двух остроугольных вершин.
Их пересечение создает треугольник ВDC:
Угол ∠ABC =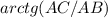
Значит ∠DBC =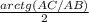
Угол ∠BCA =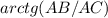
Значит ∠DCA =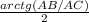 .
.
Напишем уравнение прямой BC
где BA =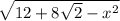 , AC = x
, AC = x
Теперь, зная что центр вписанной окружности находится на одинаковом расстоянии от сторон треугольника, напишем систему равенств.
Теперь ищем такое значение Dx, при котором Dx = расстоянию от точки D то прямой BC.
Расстояние от точки D то прямой BC будет равно по формуле
Составим систему равенств
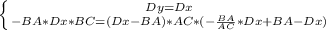
Не решайте такА теперь приступим к настоящему :
Так как гипотенуза равна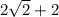 и один из катетов например AC = x, то катет AB =
и один из катетов например AC = x, то катет AB = 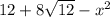
Проводим биссектрисы из прямой и остроугольной вершины.
Их пересечение создает треугольник ADC:
Угол ∠BAC = 90°
Значит ∠DAC = 45°
Угол ∠BCA =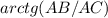
Значит ∠DCA =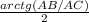 .
.
Найдем значение x1 при котором прямые AD и DC пересекаются:
x1 =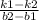 , где k1 и b1 коэффициенты прямой AD а k2 и b2 коэффициенты прямой DC.
, где k1 и b1 коэффициенты прямой AD а k2 и b2 коэффициенты прямой DC.
Площадь треугольника BDC равно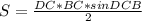 .
.
А радиус окружности равен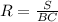
Подставим все известные нам величины.
Я сам в шоке.
Я не просто в шоке, а в полном отчаянии, потому что нам сейчас надо найти производную от этого.
Самое обидное то, что я знаю какой будет ответ, а именно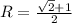
потому что максимальный радиус будет при равных катетах прямоугольного треугольника.
Но обоснование ответа будет мне стоить похоже 10 лет жизни.
прощения. Я не смог вам с решением данной задачи