На сфере проведены две окружности (рис. 7 .12). 1.На сколько частей разделена сфера данными окружностями?
2.Сколько точек пересечения у этих окружностей?
*

Показать ответ

Ответ:

SonyEricsson

08.02.2021 02:44

Рассмотрим функцию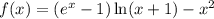 $f(x)=(e^x-1)\ln(x+1)-x^2$ .

Область определения функции: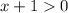 x+10 откуда x-1 .

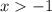Исследуем функцию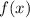 f(x) на монотонность. Ищем производную функции

$f'(x)=e^x\ln(x+1)+\dfrac{e^x-1}{x+1}-2x=0$

$e^x\ln(x+1)+\dfrac{e^x-1}{x+1}=2x$

Строим график функции стоящую слева в уравнении - возрастающая (на области определения) и прямую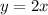 y=2x . Графики пересекаются только в одной точке (0;0).

(-1)___-____(0)_____+____

При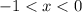 производная отрицательная, а при 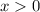- положительная. Следовательно, функция 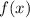f(x) на промежутке 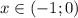$x \in (-1;0)$ убывает, а на пром. 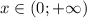$x \in (0;+\infty)$ - возрастает. Значит, в точке 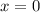x=0 функция имеет максимум, который равный 0

Следовательно, функция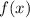 f(x) всюду положительна на области определения и кроме точки 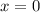x=0 , получаем

$f(x)0~~\Rightarrow~~~ (e^x-1)\ln (1+x)-x^20~~\Rightarrow~~ (e^x-1)\ln(1+x)x^2$

Докажите неравенство: (e^x - 1)*ln(1+x)>x^2

0,0(0 оценок)

Ответ:

AshesSpy

30.04.2021 04:56

Зачем я выделил в решении три цвета? Розовый, желтый и синий?

1. Розовый - это начальные условия. Т.е. Задача Коши здесь решается. И дается нач. условие, чтобы найти с.

2. Желтый, для решения линейного диф. уравнения первого порядка вводят переменные u и v, которые подлежат определению.

3. Синий. При нахождении ∫㏑х dx опять вводим u и v, интегрируя по частям, но это уже совсем другие u и v, нежели те, что вводятся для решения линейного диф. уравнения.

В этом надо Вам хорошенько разобраться, если хотите научиться решать такие задания. Удачи.