Пошаговое объяснение:
4. Если диагонали четырехугольника пересекаются в одной точке и пересечения делятся в ней пополам, то четырехугольник - параллелограмм,
диагональ МК х=(2+6)/2=4; у=(2+6)/2=4 (4; 4)
диагональ NР х=(5+3)/2=4; у=(3+5)/2=4 (4; 4)
Точки совпали (4; 4) - является середина диагонали, следовательно MNKP - параллелограммом.
5. Мы знаем, что у ромба все стороны равны, следовательно рассмотрит векторы его сторон:
вектор MN=(5-2;3-2)=(3;1)
вектор NK=(6-5;6-3)=(1;3)
вектор KР=(3-6; 5-6)=(-3;-1)
вектор РМ=(3-2; 5-2) = (1;3)
Получаем, что MN=NK=KP=PM, а из этого следуют что MNPK - квадрат, по определению.
Но, по свойству ромба, у него диагонали не равны, следовательно рассмотрим векторы -диагонали.
МК=(6-2; 6-2) = (4;4) и NP=(3-5; 5-3)=(-2 ;2)
Из этого следует, что диагонали квадрата не равны, следовательно это ромб, по определению
До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
1) Производная произведения:
Правило дифференцирования сложной функции: (индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
тогда
2) Дифференцирование сложной функции
Примем
Дифференцируем f(g):
Дифференцируем g(x):
Тогда
3) Как и в 2, дифференцируем сложную функцию
4) Производная суммы есть сумма производных:
Окончательно
5) Опять производная сложной функции:
Пошаговое объяснение:
4. Если диагонали четырехугольника пересекаются в одной точке и пересечения делятся в ней пополам, то четырехугольник - параллелограмм,
диагональ МК х=(2+6)/2=4; у=(2+6)/2=4 (4; 4)
диагональ NР х=(5+3)/2=4; у=(3+5)/2=4 (4; 4)
Точки совпали (4; 4) - является середина диагонали, следовательно MNKP - параллелограммом.
5. Мы знаем, что у ромба все стороны равны, следовательно рассмотрит векторы его сторон:
вектор MN=(5-2;3-2)=(3;1)
вектор NK=(6-5;6-3)=(1;3)
вектор KР=(3-6; 5-6)=(-3;-1)
вектор РМ=(3-2; 5-2) = (1;3)
Получаем, что MN=NK=KP=PM, а из этого следуют что MNPK - квадрат, по определению.
Но, по свойству ромба, у него диагонали не равны, следовательно рассмотрим векторы -диагонали.
МК=(6-2; 6-2) = (4;4) и NP=(3-5; 5-3)=(-2 ;2)
Из этого следует, что диагонали квадрата не равны, следовательно это ромб, по определению
До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
Пошаговое объяснение:
1) Производная произведения: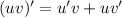
Правило дифференцирования сложной функции: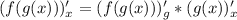 (индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
(индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
тогда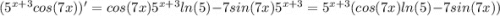
2) Дифференцирование сложной функции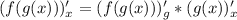
Примем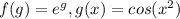
Дифференцируем f(g):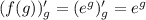
Дифференцируем g(x):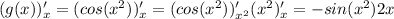
Тогда
3) Как и в 2, дифференцируем сложную функцию
4) Производная суммы есть сумма производных:
Окончательно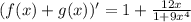
5) Опять производная сложной функции: