Войти
АнонимМатематика20 января 18:46
Сарай имеет форму прямоугольного параллелепипеда. Ширина сарая 7,5 м, длина – в 1,68 раза больше ширины, а высота – на
9,4 м меньше длины. Сарай заполнен сеном. Чему равна масса этого сена, если 1м³ сена весит 0,6 ц?
ответ или решение1
Тетерина Татьяна
1. Узнаем, чему равна длина сарая, если она в 1,68 раз больше ширины:
7,5 м * 1,68 = 12,6 м.
2. Теперь узнаем высоту сарая, отняв от длины сарая 9,4 метра:
12,6 м - 9,4 м = 3,2 метра.
3. Выясним объем сарая, умножив его высоту на длину на ширину, получим:
7,5 м * 12,6 м * 3,2 м = 302,4 м3.
4. Теперь можем рассчитать массу сена в сарае, если в 1 м3 помещается 0,6 ц сена, тогда получим:
302,4 м3 * 0,6 ц = 181,44 ц.
ответ: масса сена в сарае составляет всего 181,44 ц.
Пусть a = x - d, b = x, c = x + d, где d - разность прогрессии. Известно,
что SΔ = , где Р - периметр треугольника; по условию R•г = 130
⇒ R = 130/r ⇒ abc·r/(4·130) = (a + b + c)·r/2 ⇒ abc = 260·(a + b + c) ⇒
(x - d)·x·(x + d) = 260·(x - d + x + x + d) ⇔ x(x² - d²) = 3·260x ⇒
x(x² - d² - 780) = 0 ⇒ x² = d² + 780, так как сторона Δ положительна.
По условию (а, b, с) – тройка целых чисел ⇒ подбираем d так, чтобы было целым и наименьшим из возможных;
при d = 2 имеем: х = = 28 ⇒ a = 28 - 2 = 26; b = 28; c = 28 + 2 = 30
⇒ (26; 28; 30) – наименьшая целая тройка сторон треугольника.
Войти
АнонимМатематика20 января 18:46
Сарай имеет форму прямоугольного параллелепипеда. Ширина сарая 7,5 м, длина – в 1,68 раза больше ширины, а высота – на
9,4 м меньше длины. Сарай заполнен сеном. Чему равна масса этого сена, если 1м³ сена весит 0,6 ц?
ответ или решение1
Тетерина Татьяна
1. Узнаем, чему равна длина сарая, если она в 1,68 раз больше ширины:
7,5 м * 1,68 = 12,6 м.
2. Теперь узнаем высоту сарая, отняв от длины сарая 9,4 метра:
12,6 м - 9,4 м = 3,2 метра.
3. Выясним объем сарая, умножив его высоту на длину на ширину, получим:
7,5 м * 12,6 м * 3,2 м = 302,4 м3.
4. Теперь можем рассчитать массу сена в сарае, если в 1 м3 помещается 0,6 ц сена, тогда получим:
302,4 м3 * 0,6 ц = 181,44 ц.
ответ: масса сена в сарае составляет всего 181,44 ц.
Пусть a = x - d, b = x, c = x + d, где d - разность прогрессии. Известно,
что SΔ =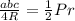 , где Р - периметр треугольника; по условию R•г = 130
, где Р - периметр треугольника; по условию R•г = 130
⇒ R = 130/r ⇒ abc·r/(4·130) = (a + b + c)·r/2 ⇒ abc = 260·(a + b + c) ⇒
(x - d)·x·(x + d) = 260·(x - d + x + x + d) ⇔ x(x² - d²) = 3·260x ⇒
x(x² - d² - 780) = 0 ⇒ x² = d² + 780, так как сторона Δ положительна.
По условию (а, b, с) – тройка целых чисел ⇒ подбираем d так, чтобы было целым и наименьшим из возможных;
было целым и наименьшим из возможных;
при d = 2 имеем: х =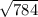 = 28 ⇒ a = 28 - 2 = 26; b = 28; c = 28 + 2 = 30
= 28 ⇒ a = 28 - 2 = 26; b = 28; c = 28 + 2 = 30
⇒ (26; 28; 30) – наименьшая целая тройка сторон треугольника.