Здесь я позволю себе подробно расписать получение элементов при умножении матриц, но обычно все расчеты проводят усно и так лучше не шутить:)
а)
б)
в) Перед поиском обратной матрицы проверим, существует ли она вообще. Поскольку обратные существуют только для невырожденных матриц, рассчитаем определитель и выясним, равен ли он нулю.
Итак, A^-1 существует. Найдем ее. Для начала транспонируем A:
Теперь заменим каждый элемент на его минор и умножим полученную матрицу на число, обратное определителю. Я опять-таки сделаю все подробно, но повторять не стоит:)
Если мы сделали все правильно, то после умножения обратной матрицы на A (либо наоборот) получим единичную матрицу. Это как раз и предлагают провернуть в двух последних пунктах.
Необходимое условие экстремума функции одной переменной.
Уравнение f'0(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) < 0
то точка x* - локальный (глобальный) максимум.
Находим первую производную функции:
y' = -x2+6
Приравниваем ее к нулю:
-x^2+6 = 0
-x^2=-6
x^2=6
x1,2=+/-√6
Вычисляем значения функции:
f(-√6)=-4√6+7
f(√6)=7+4√6
Нам нужно fmax:
fmax=7+4√6
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
Пошаговое объяснение:
Здесь я позволю себе подробно расписать получение элементов при умножении матриц, но обычно все расчеты проводят усно и так лучше не шутить:)
а)
б)
в) Перед поиском обратной матрицы проверим, существует ли она вообще. Поскольку обратные существуют только для невырожденных матриц, рассчитаем определитель и выясним, равен ли он нулю.
Итак, A^-1 существует. Найдем ее. Для начала транспонируем A:
Теперь заменим каждый элемент на его минор и умножим полученную матрицу на число, обратное определителю. Я опять-таки сделаю все подробно, но повторять не стоит:)
Если мы сделали все правильно, то после умножения обратной матрицы на A (либо наоборот) получим единичную матрицу. Это как раз и предлагают провернуть в двух последних пунктах.
г)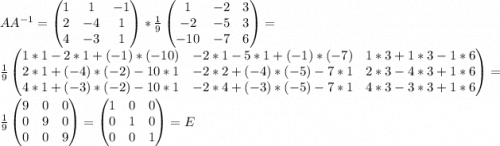 д)
д)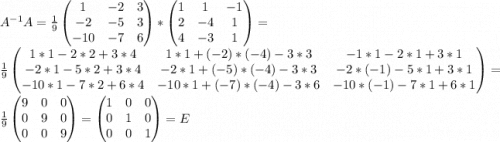
Уравнение f'0(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) < 0
то точка x* - локальный (глобальный) максимум.
Находим первую производную функции:y' = -x2+6
Приравниваем ее к нулю:-x^2+6 = 0
-x^2=-6
x^2=6
x1,2=+/-√6
Вычисляем значения функции:f(-√6)=-4√6+7
f(√6)=7+4√6
Нам нужно fmax:fmax=7+4√6
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:y'' = -2·x
Вычисляем:y''=(√6)=-2√6<0
Значит это точка максимума функции.ответ:√6