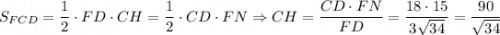мне решить планиметрическую задачу типажа номер 16 из ЕГЭ. Дана трапнция ABCD, где M и N - середины боковых сторон AB и CD. На стороне AD выбрана точка F такая, что угол FMC - прямой и MN = CF. а) Доказать, чтоMF||CD. б) Найти площадь ABCD, если tg угла FCM = 3/5, а MC = 15.
Заранее благодарю.
б) 270
Пошаговое объяснение:
а) Пусть MN ∩ CF = O. MN — средняя линия ABCD ⇒ MN || AD. По теореме Фалеса MN || AD, CN = ND ⇒ CO = OF. В прямоугольном треугольнике CMF MO — медиана ⇒ MO = CF / 2 = MN / 2 ⇒ MO = ON. В четырёхугольнике CMFN CO = OF, MO = ON ⇒ CMFN — параллелограмм ⇒ MF || CN ⇒ MF || CD, что и требовалось доказать.
б) В прямоугольном треугольнике CMF tg ∠FCM = MF / MC = MF / 15 = 3 / 5 ⇒ MF = 9 ⇒ CD = 2CN = 2MF = 18. CF² = CM² + MF² = 9² + 15² = 306 ⇒ CF = √306 = 3√34 = MN. MF || CD, MF = CN = ND ⇒ MFDN — параллелограмм ⇒ FD = MN = 3√34.
CMFN — параллелограмм ⇒ ∠CMF = ∠FNC = 90° ⇒ FN ⊥ CD.
Пусть CH — высота трапеции, а значит, и треугольника FCD. Тогда