Мне нужно с решением Сколько различных «слов» из трёх букв можно составить
из букв слова ЗАЧЁТ?

a) x = 38

б) x = 1125

в) x = 1025

D) x = 3188

е) x = 16

е(2)) x = 32

G) x = 17

з) x = 58

Пошаговое объяснение:

a)

x + 453 = 491

x = 491 - 453

x = 38

б)

4578 - x = 3453

-x = 3453 - 4578

-x = -1125

x = 1125

в)

x - 678 = 347

x = 347 + 678

x = 1025

D)

x + 4379 = 7567

x = 7567 - 4379

x = 3188

е)

16x = 256

16x : 16 = 256 : 16

x = 16

е(2))

1024 : x = 32

1024 : x = 32, x 0

= 32

1024 = 32x

32x = 1024

x = 32, x 0

x = 32

G)

5202 : x = 306

5202 : x = 306, x 0

= 306

5202 = 306x

306x = 5202

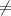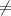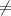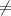x = 17, x 0

x = 17

з)

46x = 2668

46x : 46 = 2668 : 46

x = 58

ответ: Шаг 1: находим координаты х точек перечечения графиков y=x^2+1 и y=-x+3.

x^2+1 = -x+3; x^2+x-2 = 0; x1 = -2; x2 = 1.

Шаг 2: Находим определенный интеграл функции y = -x+3 в пределах от -2 до 1.

Первообразная этой функции будет Y = -1/2*x^2 + 3x + С

Подставляя пределы интегрирования получаем площадь под функцией S1 = -1/2 + 3 + 2 + 6 = 10,5.

Шаг 3: Находим определенный интеграл функции y = x^2+1 в пределах от -2 до 1.

Первообразная этой функции будет Y = 1/3*x^3 + x + С

Подставляя пределы интегрирования получаем площадь под функцией S2 = 1/3 + 1 + 8/3 +2 = 6.

Шаг 4: S = S1-S2; S = 10,5-6; S = 4,5.

Пошаговое объяснение: