Математическая логика! Второй курс
Задание:
Пусть А, В и С - множестваа точек плоскости, координаты которых удовлетворяют условиям
a. b и y соответственно. Изобразите в системе координат х0у множество D, полученное из множеств
A, В и С по формуле б.
Варианты 4, 8 и 10 (фото прилагается)
2) 120 уч.
3) 90 очков
4) 40 уч.
Пошаговое объяснение:
Первая задача.Кр.запись.
250 руб - было всего
120 руб - потратила
? - часть своих денег Маша заплатила за мороженое
Решение.
120 / 250 =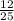
- Маша заплатила за мороженое
Вторая задача.Кр. запись.
420 уч. - всего
? уч. - ходят в муз. школу, но сказано, что ходят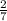
от всего кол-ва
Решение.
420 *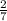
= 420 : 7 * 2 = 120 уч. - ходят в муз. школу
Третья задача.Кр. запись.
24 очка - получил капитан
? очков - получила команда, но сказано, что капитан получил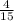
всех полученных очков.
Решение.
24 :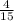
= 24 * 
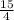= 24 : 4 * 15 = 90 очков - получила команда
Четвёртая задача.Кр.запись
в 3 классах поровну учащихся
? уч. - в каждом классе, но сказано, что если в каждый класс добавить по 3 уч., то всего в них будет 129 уч
Решение.
3 * 3 = 9 уч. - добавили
129 - 9 = 120 уч. - в 3 классах
120 : 3 = 40 уч. - в каждом классе.
Корень четвёртой степени из 2 вряд-ли получится извлечь. Чтобы сравнивать числа разных "типов", необходимо их привести к одному единому. Так, мы сравниваем числа 1 и корень 4 степени из 2. Так как второе мы извлечь не можем, будем работать с первым. Мы знаем, что единица в любой степени равна себе же. Значит, мы ее можем представить, как корень 4 степени из 1. Теперь давайте условно отбросим корень и сравним числа 2 и 1. Получим, что 2 больше 1. Таким образом, корень 4 степени из 2 больше одного