Проверим, может ли при каких-то a и b из G получиться в результате операции число не из G (то есть -1, так как, очевидно, результат операции - действительное число)
То есть посредством операции нельзя выйти из R\{-1}
Найдем нейтральный элемент по этой операции:
- нейтральный элемент существует
Проверим свойство ассоциативности:
- выполнено
Посмотрим, у каждого ли есть обратный элемент. Рассмотрим произвольный элемент a:
Обратный существует (так как a не равен -1), а также , то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
Ситуация 1:(наименьшее количество работников работающих это те кто знают оба языка)15% человек знают оба языка.
Ситуация 2:(это те кто знают французский)15%
(Думаю 2-ое правильней)
Пошаговое объяснение:
Первая ситуация:
(Вопрос странный, но если я правильно понял то вот)
1)28+23=51% (человек знают испанский)
2)15%(человек знает французский)
3)(Если 100% людей знающих французский знают испанский то)
100-51=49% (не знают языков)
(а значит 15%человек знают оба языка, а значит 51-15=36% человек знают только испанский)
Или 2-ая ситуация:
1,2)КАК В ПЕРВОМ
3)(Если 100% людей знающих испанский не знают французский то)
51+15=66%(всего человек знающих иностранный язык)
4)100-66=34%(не знают языков)
(Если-бы вопрос был таким скок процентов рабочих не нужны то)
Всё как в первой ситуации, но с ответом 49% так как они не знают языков,а во втором все как во второй ситуации, ну только 34% не знают языков
Заметим для начала, что операция коммутативна
Проверим, может ли при каких-то a и b из G получиться в результате операции число не из G (то есть -1, так как, очевидно, результат операции - действительное число)
То есть посредством операции нельзя выйти из R\{-1}
Найдем нейтральный элемент по этой операции:
Проверим свойство ассоциативности:
Посмотрим, у каждого ли есть обратный элемент. Рассмотрим произвольный элемент a:
Обратный существует (так как a не равен -1), а также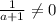 , то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
, то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
Таким образом, G - абелева группа.