Пошаговое объяснение:
708
1)0,04х=2
х=2:0,04
x=50
2)0,132x=132
x=132:0,132
x=1000
3)17,5x=0,63
x=0,63:17,5
x=0,036
4)0,34x=10,54
x=10,54:0,34
x=31
5)0,32x=16,48
x=16,48:0,32
x=51,5
6)1,2x=4,02
x=4,02:1,2
x=3,35
709
1)4,37:1,9+8,78=11,08
4,37:1,9=2,3
2,3+8,78=11,08
2)7,91-6,72:1,2=2,31
6,72:1,2=5,6
7,91-56=2,31
3)6,88:1,6-3,99=0,31
6,88:1,6=4,3
4,3-3,99=0,31
4)10,05+7,31:1,7=14,35
7,31:1,7=4,3
10,05+4,3=14,35
5)85,8:0,33-258,1=1,9
85,8:0,33=260
260-258,1=1,9
6)1,968:0,41+28,2=33
1,968:0,41=4,8
4,8+28,2=33
Для того чтобы высчитать площадь фигуры неразрывной функции на некотором промежутке, следует воспользоваться формулой Ньютона — Лейбница:
Здесь и — границы фигуры на оси абсцисс, — первообразная для функции
квадратных единиц.
2) Здесь имеем площадь фигуры, ограниченной двумя функциями: и .
Чтобы найти данную площадь, нужно найти разность площадей каждой функции.
Очевидно, что площадь фигуры, образованной функцией на отрезке больше, чем площадь фигуры, образованной функцией на том же отрезке, поэтому
Пошаговое объяснение:
708
1)0,04х=2
х=2:0,04
x=50
2)0,132x=132
x=132:0,132
x=1000
3)17,5x=0,63
x=0,63:17,5
x=0,036
4)0,34x=10,54
x=10,54:0,34
x=31
5)0,32x=16,48
x=16,48:0,32
x=51,5
6)1,2x=4,02
x=4,02:1,2
x=3,35
709
1)4,37:1,9+8,78=11,08
4,37:1,9=2,3
2,3+8,78=11,08
2)7,91-6,72:1,2=2,31
6,72:1,2=5,6
7,91-56=2,31
3)6,88:1,6-3,99=0,31
6,88:1,6=4,3
4,3-3,99=0,31
4)10,05+7,31:1,7=14,35
7,31:1,7=4,3
10,05+4,3=14,35
5)85,8:0,33-258,1=1,9
85,8:0,33=260
260-258,1=1,9
6)1,968:0,41+28,2=33
1,968:0,41=4,8
4,8+28,2=33
Для того чтобы высчитать площадь фигуры неразрывной функции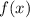 на некотором промежутке, следует воспользоваться формулой Ньютона — Лейбница:
на некотором промежутке, следует воспользоваться формулой Ньютона — Лейбница:
Здесь и
и 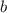 — границы фигуры на оси абсцисс,
— границы фигуры на оси абсцисс, 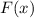 — первообразная для функции
— первообразная для функции 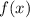
2) Здесь имеем площадь фигуры, ограниченной двумя функциями: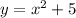 и
и 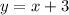 .
.
Чтобы найти данную площадь, нужно найти разность площадей каждой функции.
Очевидно, что площадь фигуры, образованной функцией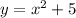 на отрезке
на отрезке ![[-2; \ 1]](/tpl/images/1068/9083/4704b.png) больше, чем площадь фигуры, образованной функцией
больше, чем площадь фигуры, образованной функцией 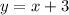 на том же отрезке, поэтому
на том же отрезке, поэтому