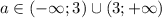а) Если даны две функции, у которых коэффициент k (стоящий перед x) равен, то графики этих функций будут параллельны.
У первой функции k = a/2, у второй - 1,5. Для того, чтобы коэффициенты были равны, нужно подставить такое значение a, чтобы при делении на 2 оно давало 1,5.
В таком случае, a = 3.
б) Если даны две функции, не имеющих равных коэффициентов k и m (то есть она не будут параллельны или одна функция не равна другой), то у графиков этих функций будет одна общая точка. В таком случае, a может принять любое значение, кроме 3 (иначе графики будут параллельны).
- 7 кН
20 кН
-31 кН*м
Пошаговое объяснение:- 7 кН
20 кН
-31 кН*м
Объяснение:
Сделаем чертеж.
Раскладываем силу F₁ на вертикальную и горизонтальную составляющую по теореме Вариньона:
F₁y = F₁*sin 60⁰ = 14*√3 / 2 ≈ 12 кН
F₁ₓ = F₁*cos 60⁰ = 14*1 / 2 ≈ 7 кН
1)
Сумма проекций всех сил на ось OX должна равняться нулю.
∑Fₓ = Nₓ + F₁ₓ = 0
Nₓ = - F₁ₓ = - 7 кН
Знак "-" говорит о том, что реакция заделки направлена противоположно
2)
Сумма проекций всех сил на ось OY должна равняться нулю.
∑Fy = Ra - F₁y - F₂ = 0
Ra = F₁y + F₂ = 12 + 7,8 ≈ 20 кН
3)
Сумма моментов всех сил относительно точки A должна равняться нулю:
∑Ma = - MA - F₁y*AB - F₂*AC - m = 0
- MA - 12*0,6 - 7,8*1,5 - 12 = 0
MA ≈ - 31 кН*м
Знак "-" говорит о том, что момент заделки направлен противоположно указанному на чертеже.
Проверку сделайте самостоятельно: найдите сумму моментов относительно точки В. Она должна быть равна нулю!.
(Подсказка: -12+12*0,9+20*1,5-31 = -2,2 ≈ 0. Несовпадение вызвано погрешностью вычислений).
а) Если даны две функции, у которых коэффициент k (стоящий перед x) равен, то графики этих функций будут параллельны.
У первой функции k = a/2, у второй - 1,5. Для того, чтобы коэффициенты были равны, нужно подставить такое значение a, чтобы при делении на 2 оно давало 1,5.
В таком случае, a = 3.
б) Если даны две функции, не имеющих равных коэффициентов k и m (то есть она не будут параллельны или одна функция не равна другой), то у графиков этих функций будет одна общая точка. В таком случае, a может принять любое значение, кроме 3 (иначе графики будут параллельны).
То есть,