класс решите все 1. выразить в радианной степени величины углов
2. выразить в градусной степени величины углов
3. изобразите угол, образованный поворотом луча ОА вокруг точки О на

упростить выражение и доказать тождество
найдите знак выражения

Если мы ищем производную по х то ответ будет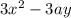

Если мы ищем производную по у то ответ будет

Если мы берём производную по а то ответ будет просто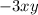

Так же производную невозможно искать если приравнивать к нулю.

Рассчитывал производную  по основной формуле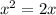 . Если мы берём производную от степени то уменьшаем её на 1 и выносим изначальное число степени перед иксом.

А так же если у мы берём допустим по х то там где просто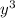  то это равно 0 и мы не учитываем, а если есть х и у то смотрим на степень х и у и действуем по схеме выше. Так как у нас в конце стоит 3ху и х и у в первой степени, то мы просто убираем либо х либо у, и оставляем либо х либо у.

Пошаговое объяснение:

Проиллюстрируйте с кругов Эйлера высказывание: «Все

учащиеся 5 класса присутствовали на школьной спартакиаде».

Решение: Выделим множества, о которых идет речь в высказывании:

это множество учащихся некоторой школы

(обозначим его за А), и множество учащихся 5 класса

(обозначим его В). В данном высказывании утверждается,

что все элементы множества В являются также и

элементами множества А. По определению отношения включения

это означает, что В А. Поэтому множество В надо изобразить внутри круга,

изображающего множество А.

2. Задайте множество другим если это возможно):

а) А = {х| xN, х ≤ 9}; б) А = {-4, -3, -2, -1, 0, 1, 2, 3, 4};

в) А = {х| xR, х

2

– 3 = 0}.

Решение: а) Элементами множества А являются натуральные числа,

которые меньше 9 и само число 9, значит, А = {1, 2, 3, 4, 5, 6, 7, 8, 9};

б) А = {х| xZ, |x| ≤ 4} – множество целых чисел, модуль которых не

больше четырех;

в) Элементами множества А являются корни уравнения х

2

– 3 = 0,

значит, А = {- 3 , 3 }.

3. Изобразите на координатной прямой перечисленные множества:

а) А = {х| xR, -1,5 ≤ х ≤ 6,7}; б) М = {х| xN, 4х - 14 < 0};

в) С = {х| xZ, -5 < х <2}; г) Н = {х| xZ, |x| < 7}.

Решение: ответы показаны на рисунке:

а) А = [-1,5; 6,7]

б) М = {1, 2, 3}

в) С = (-5; 2)

г) Н = {-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}

4. Задайте числовое множество описанием характеристического

свойства элементов: а) (0; 11); б) [-12,3; 1,1); в) [-5; 3]; г) (- ∞; -102,354].

а) А = {х| xR, 0 < х <11}; б) С = {х| xR, -12,3 ≤ х < 1,1};

в) А = {х| xR, -5 ≤ х ≤ 3}; г) Р = {х| xR, х ≤ -102,354}.

5. Даны множества:

а) К = {у| у = 1, если уN, то у + 1N}