Класс - 30 - 61 =+-
-6-65=
30-61 = 1.4
56-65 =
-1 -7= 6、+
-3-29=
-12 +9=3+ -13 -89=
18 - (9) =
一
3-89-
- 40 +6=-30 + 22 - 01-28) =
21 - (-1) = 420 12 + 21 = +9+
91-8=
15.95 =
-1-8 =+
-15 +5 =
- 59 +3 = -2 22-28 =
40 -(-10) =
71 + 0=
40 + (-10) =
-- 70 =
-1-5 = f. 70 - (-29) =
33 - 1-16) = 197 -70 - (1-29) =
33 - (-16) =
55 + (-25) =
- 14-14 =
55-(-22) =
14 - 14=13.
89-19=
-1-1 =
18-98 -
1+1=a
60 -(-21) =
-1-11 =
- 4 - 19=
45 - (-18) =
-1-19=
20 + (-15) =
- 4-60 =
36-74-
71489 =
27-7-34) =
-7-67=
31-51=
1-51=
23 - (35) =
-5-81 =
-62-2=
62-2=
- 0-96=
-9-29 :
-2-23 -
3 + (-8)=
-80-2=
98-1-9) =
-24-64 =
9-1-11) =
-72-9=
3-6-
3-1-20) -
307-=
- 22-8=
50 -(-970) =
61-911-
01-01-
269-5=
-34-4-
-20 - -320) =
- 288 - 14 =
240 - (-30) =
512-2 =
230-1-320) =
70 - 17 =
106 - (-3)=
-1 - 91 =
-109-1=
- 17-66=
-333-33=
500-6=
602 - (-8)=
369 -(-8)=
-
-

Показать ответ

Ответ:

prostooo202003

22.05.2020 15:51

Пошаговое объяснение:

сначала всегда действия в скобочках 80:16=5

затем деление (умнодение) ,если их несколько то идут по порядку ,получаеться 1100:25=44

ечли сразу псоле этого децствие деление то результат делим ,то есть 44:11=4

затем пропускаем сумму и идем дальше к делению ,делим 600 на результате который был в скобочках и получаем 600:5=120,

затем дальше полученный результат делим на следущее число и получаес 120:12=10

и последнее слаживаем две части(результат до плюса и результат после плюса) и получаем 4+10=14

0,0(0 оценок)

Ответ:

анн57

07.03.2023 15:47

ответ:Чтобы решить это уравнение, разделите знаменатели на множители и с квадратичной формулы найдите два действительных корня, которые дадут значение x.

Пошаговое объяснение:

Чтобы решить это уравнение, нужно разложить знаменатели дробей. Уравнение имеет вид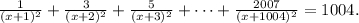 $\frac{1}{(x+1)^2} + \frac{3}{(x+2)^2} + \frac{5}{(x+3)^2} + \dotsb + \frac{2007}{(x+1004)^2} = 1004.$ Затем мы можем умножить обе стороны уравнения на (x+1)^2(x+2)^2...(x+1004)^2 и разложить левую часть, в результате чего получим полиномиальное уравнение степени 1004. Чтобы решить это уравнение, нам нужно воспользоваться квадратичной формулой для нахождения корней многочлена. В результате мы получим два вещественных корня, которые и дадут значение x.

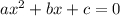Квадратичная формула - это математическое уравнение, используемое для решения корней полиномиального уравнения степени два. Она гласит, что для любого квадратного уравнения. ax^2 + bx + c = 0 два корня можно найти по следующей формуле: x = (-b ± √(b^2 - 4ac)) / 2a, где a, b и c - коэффициенты полиномиального уравнения. Знак ± указывает на то, что уравнение может иметь два различных решения в зависимости от выбранного знака.