Кестедегі мәлеметтер мен сызбаны пайдаланып, кездесу қозғалысына және қарама-қарсы қозғалысқа есептер құрастыр

Показать ответ

Ответ:

potapovp016

21.06.2021 09:48

а) да; б) нет; в) 972

Пошаговое объяснение:

а) Пусть геометрическая прогрессия имеет знаменатель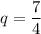 $q=\dfrac{7}{4}$ . Тогда получим последовательность 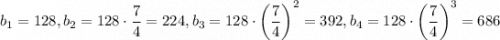$b_1=128,b_2=128\cdot\dfrac{7}{4}=224,b_3=128\cdot\left(\dfrac{7}{4}\right)^2=392,b_4=128\cdot\left(\dfrac{7}{4}\right)^3=686$ . Число 686 может быть записано на доске.

б) Заметим, что знаменатель прогрессии q не может быть иррациональным числом: в противном случае второй член прогрессии b₂ = 128q — иррациональное число, что противоречит условию. Значит, q — рациональное число.

Предположим, что 496 является n-ным членом последовательности. Тогда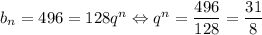 $b_n=496=128q^n\Leftrightarrow q^n=\dfrac{496}{128}=\dfrac{31}{8}$ . Поскольку 31 — простое число, оно не является степенью какого-либо другого числа. Значит, n = 1, 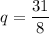$q=\dfrac{31}{8}$ . Тогда получаем геометрическую прогрессию 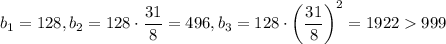$b_1=128,b_2=128\cdot\dfrac{31}{8}=496,b_3=128\cdot\left(\dfrac{31}{8}\right)^2=1922999$ — третий член последовательности не трёхзначный, что противоречит условию. Значит, прогрессии с членом 496 не существует.

в) Пусть A — наибольший возможный член геометрической прогрессии, по условию A < 1000. Тогда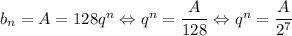 $b_n=A=128q^n\Leftrightarrow q^n=\dfrac{A}{128}\Leftrightarrow q^n=\dfrac{A}{2^7}$ . Число 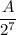$\dfrac{A}{2^7}$ является степенью некоторого рационального числа, значит, 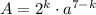$A=2^k\cdot a^{7-k}$ , где k — некоторое целое число из промежутка [0, 7], a — положительное нечётное число. Число представимо в таком виде, поскольку на 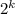2^k можно сократить, в знаменателе останется 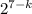$2^{7-k}$ , далее дробь несократима и является степенью n = 7 - k числа q: 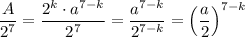$\dfrac{A}{2^7}=\dfrac{2^k\cdot a^{7-k}}{2^7}=\dfrac{a^{7-k}}{2^{7-k}}=\left(\dfrac{a}{2}\right)^{7-k}$ . 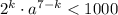Значит, $2^k\cdot a^{7-k}$ .

Переберём все k от 0 до 7:

k = 0:

. $2^7=128,3^7=2187\Rightarrow a\leq 2\Rightarrow a\leq 1\Rightarrow A\leq 1$ k = 1: 2a^6

. $2^6=64, 3^6=729\Rightarrow a\leq 2\Rightarrow a\leq 1\Rightarrow A\leq 2$ k = 2: 4a^5

. $3^5=243,4^5=1024\Rightarrow a\leq 3\Rightarrow A\leq 972$ k = 3: 8a^4

. $3^4=81,4^4=256\Rightarrow a\leq 3\Rightarrow A\leq 648$ k = 4: 16a^3

. $3^3=27, 4^3=64\Rightarrow a\leq 3\Rightarrow A\leq 432$ k = 5: 32a^2

. $5^2=25,6^2=36\Rightarrow a\leq 5\Rightarrow A\leq 800$ k = 6: 64a

k = 7:

— верно, A = 128.

Наибольшее значение A = 972. Покажем, что оно достигается. Пусть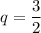 $q=\dfrac{3}{2}$ . Тогда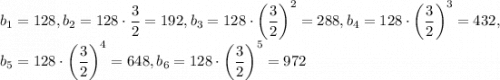 $b_1=128,b_2=128\cdot\dfrac{3}{2}=192,b_3=128\cdot\left(\dfrac{3}{2}\right)^2=288,b_4=128\cdot\left(\dfrac{3}{2}\right)^3=432,\\b_5=128\cdot\left(\dfrac{3}{2}\right)^4=648,b_6=128\cdot\left(\dfrac{3}{2}\right)^5=972$

Таким образом, наибольшее число, которое могла выписать Даша — 972.

0,0(0 оценок)

Ответ:

LOLLIPOPS45

08.06.2023 16:54

Sполн=1032 см²

V=1512 см3

Пошаговое объяснение:

V=Sосн*H

S oсн=√ (p * (p-a) * (p-b) * (p-c))

p=P/2. P=a+b+c

p = (10+17+21) / 2

p=24

S=√ (24 * (24-10) * (24-17) * (24-21))

S=84

V=84*18

Площадь боковой поверхности треугольной призмы будет:

Sбок=18*(10+17+21)=864 см²

Для нахождения площади основания можно воспользоваться формулой Герона для нахождения площади треугольника, когда известны только длины его сторон, но неизвестна высота:

S=√p(p-a)(p-b)(p-c) (под корнем всё выражение!), где a,b,c- стороны треугольника, p- полупериметр треугольника, p=(a+b+c)/2.

p=(10+17+21)/2=24

S=√24(24-10)(24-17)(24-21)=√24*14*7*3=√7056=84 см²

Полная поверхность призмы равна:

Sполн=Sбок+2Sосн

Sполн=864+2*84=864+168=1032 см²

Sполн=1032 см²

0,0(0 оценок)

Популярные вопросы: Математика