Составим уравнение касательной к графику функции в точке .
Значение функции в точке касания:
Найдем производную:
Значение производной в точке касания:
Уравнение касательной имеет вид:
Подставим найденные соотношения:
Так как по условию касательная проходит через начало координат, то она является прямой пропорциональностью и свободный член равен нулю:
Так как по условию абсцисса точки касания отрицательна, то остается вариант
Уравнение касательной принимает вид:
Зная, что касательная в точке касания имеет ординату 2, найдем значение m:
ответ: 3
Касательная :
Начало координат : (0 ; 0)
Подставим значения для каждого а :
Для а = 2 :
Для а = -2 :
Составим две системы уравнений (найдем точки касания ) :
1.
{
( 2 ; 8 + 2m)
Не подходит, так как x > 0, а по условию абсцисса отрицательная
2.
( -2 ; 8 - 2m)
Нам нужно, чтобы ордината = 2, то есть y = 2 :
8 - 2m = 2
2m = 8 - 2
2m = 6
m = 3
ответ : при m = 3
Составим уравнение касательной к графику функции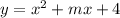 в точке
в точке 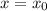 .
.
Значение функции в точке касания:
Найдем производную:
Значение производной в точке касания:
Уравнение касательной имеет вид:
Подставим найденные соотношения:
Так как по условию касательная проходит через начало координат, то она является прямой пропорциональностью и свободный член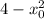 равен нулю:
равен нулю:
Так как по условию абсцисса точки касания отрицательна, то остается вариант
Уравнение касательной принимает вид:
Зная, что касательная в точке касания имеет ординату 2, найдем значение m:
ответ: 3
Касательная :
Начало координат : (0 ; 0)
Подставим значения для каждого а :
Для а = 2 :
Для а = -2 :
Составим две системы уравнений (найдем точки касания ) :
1.
{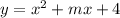
{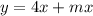
( 2 ; 8 + 2m)
Не подходит, так как x > 0, а по условию абсцисса отрицательная
2.
{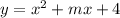
{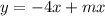
( -2 ; 8 - 2m)
Нам нужно, чтобы ордината = 2, то есть y = 2 :
8 - 2m = 2
2m = 8 - 2
2m = 6
m = 3
ответ : при m = 3