Какие свойства использовались при решении
данных примеров?
120-(20+15)=120-20-15=85 - ?
(50+12) -10=50-10+12=52 - ?
(8+52)-22=52-22+8=38 - ?​

Отношение составляющих фарфора: 6,25:0,25:0,5

Чтобы избавиться от десятичных дробей, домножим каждую часть отношения на 4 (так можно):

(6,25*4):(0,25*4):(0,5*4)

Получим отношение 25:1:2

Оно означает, что на 25 частей глины нужно взять 1 часть гипса и 2 части песка.

Пусть 1 часть=х грамм. Тогда глины надо взять 25х, песка -- 2х грамма. Их разность=184 (по условию)

Составим уравнение:

25х-2х=184

23х=184

х=8 грамм -- это 1 часть.

Значит, глины взяли 25*8=200 грамм, гипса -- 1*8=8 грамм, песка -- 2*8=16 грамм.

Общая масса чашки=200+8+16=224 грамма

ответ:224 гр.

ответ: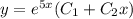

Пошаговое объяснение:

Определить общее решение дифференциального уравнения:

y" - 10y' + 25y = 0.

Решение

Характеристическое уравнение имеет вид:

k² - 10k + 25 = 0

         (k - 5)² = 0

k₁ = k₂ = 5

Корни действительные и равные k₁ = k₂ = k . В этом случае общее решение уравнения:

Определить частное решение дифференциального уравнения:  

y'+y=xy, удовлетворяющее начальному условию y(2)=5.

Решение

y' + y = xy

    y'  = xy - у

Делим обе части уравнения на у

Интегрируем обе части уравнения

ln|y| -lnC = 0.5x² - x

Запишем общее решение ДУ

Найдем частное решение ДУ подставив начальные условия y(2)=5

Поэтому частное решение ДУ