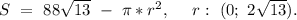Как удалить друга из бравл старса если мне говорят что друзей из социальных сетей удалить нельзя?

1)маса першого ящика рівна х+0.6 кг груш а маса другого ящика х               2) отже х+0.6+х= 24.25кг груш 24.25-0.6=23.65кг.                                         3) х= 23.65 поділити на 2 = 11.825 кг.                                                               4)маса першого ящика = 11.825+0.6+3.5=15.925 кг.                                         5)маса другого ящика 11.825-3.5=8.325 кг.                                                     провіряю правильність: 8.325+15.925= 24.25 гк. груш   

відповідь: в першому ящику 15.925 кілограмів груш а в другому ящику 8.325 кілограм груш.

якось так:)

ABCD - равноб. трапеция. АD = 31, BC = 13, AB=CD = 17. Проведем высоты: ВК и СМ.

Тогда из равенства тр-ов АВК и СМD следует, что АК = MD = (31-13)/2 = 9.

Найдем высоту из пр. тр. АВК по теореме Пифагора:

ВК = кор(AB^2-AK^2) = кор(289-81) = кор208 = 4кор13.

Найдем площадь трапеции:

s = (31+13)*(4кор13)/2 = 88кор13.

Тогда, вырезав из трапеции круг радиуса r, получим фигуру, площадью:

S = s - пr^2 = 88кор13  - пr^2. Каким может быть r?

Проверим можно ли в данную трапецию вписать окружность:

Если в 4-ник можно вписать окружность, то у него суммы противоположных сторон равны.

31+13 = 44

17+17 = 34.

Суммы не равны. Значит окружность, касающуюся всех сторон трапеции вырезать не удастся. Поэтому максимально возможное значение радиуса вырезаемой окружности равно половине высоты:

r(max) = BK/2 = 2кор13.

Итак, ответ: