Из полной колоды (36 карт) вынимают наугад одну за другой 3 карты без возвращения. Вычислить вероятность того, что: а) впервые туз появится при третьем испытании; б) все карты будут тузами; в) из трех извлеченных карт будет хотя бы 1 туз.
, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
А)) Больной ученицы нет, ее вычитаем 15-1=14 девочек и 13 мальчиков осталось; и 15девочек. Выбирать надо из всех девочек 3 девочки; Первую девочку выбираем 1 из 15 девочек; Вторую уже из 14; третью из 13;
1)) 14•13•12=2184; всех вариантов
Но девочки повторяются, девочка одна А; вторая В; третья С; =>>>> ABC; ACB; BAC; BCA; CAB; CBA; 6 раз одинаково просто местами поменяли; посчитали 6 раз одну девочку; значит делим на 6;
будет;
ответ выбрать группу из трёх человек для посещения заболевшей ученицы.
Б)) все мальчики 13; выбираем 3 из 13; первого выбираем второго на один меньше и третьего меньше на один
1)) 13•12•11= 1716;
И как с девочками повторяется 6 раз один мальчик в группе, поэтому тоже на 6 делим.
2)) 1716:6= 286
ответ выбрать группу из трёх мальчиков.
В)) Одна девочка болеет, её вычитаем 15-1=14 девочек осталось; и 13 мальчиков .
Мальчики - выбрать надо 2 из 3; первого мальчика мы выбираем 1 из 13; второго мальчика уже на 1 меньше, значит выбираем из 12; =>>>
выбрать мальчика,
но каждый мальчик посчитан два раза, просто местами поменяны как АВ и ВА одинаково пары; значит делим на 2; 2)) 156:2=78 пар мальчиков;
Девочек 1 из 14 выбираем (без больной девочки) значит любую из 14 можем выбрать =14вариантов; теперь делаем группу тройку, на каждую пару мальчиков одна девочка из 15, значит
ответ выбрать группу 3человека из два мальчика и одна девочка.
Г)) 2 девочки выбираем из 14 (одна болеет, не считаем); и 1 мальчик из 13; Девочек первую выбрать вторую
1)) 14•13=182; но каждую девочку мы посчитали два раза АВ и ВА одинаково, поменяно местами. Значит делим на 2.
выбрать две девочки.
Мальчик 1 из 13, значит любого из всех и выбираем троих девочек и мальчика умножаем,
ответ: группу 2 девочки и один мальчик можно выбрать
ответ: 180.
Вот формула площади трапеции:
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен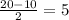 . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
. Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
Задача решена!
Выбирать надо из всех девочек 3 девочки;
Первую девочку выбираем 1 из 15 девочек; Вторую уже из 14; третью из 13;
1)) 14•13•12=2184; всех вариантов
Но девочки повторяются, девочка одна А; вторая В; третья С; =>>>> ABC; ACB; BAC; BCA; CAB; CBA;
6 раз одинаково просто местами поменяли;
посчитали 6 раз одну девочку; значит делим на 6;
будет;
ответ выбрать группу из трёх человек для посещения заболевшей ученицы.
Б)) все мальчики 13; выбираем 3 из 13; первого выбираем второго на один меньше и третьего меньше на один
1)) 13•12•11= 1716;
И как с девочками повторяется 6 раз один мальчик в группе, поэтому тоже на 6 делим.
2)) 1716:6= 286
ответ выбрать группу из трёх мальчиков.
В)) Одна девочка болеет, её вычитаем 15-1=14 девочек осталось; и 13 мальчиков .
Мальчики - выбрать надо 2 из 3;
первого мальчика мы выбираем 1 из 13;
второго мальчика уже на 1 меньше, значит выбираем из 12; =>>>
выбрать мальчика,
но каждый мальчик посчитан два раза, просто местами поменяны как АВ и ВА одинаково пары; значит делим на 2;
2)) 156:2=78 пар мальчиков;
Девочек 1 из 14 выбираем (без больной девочки) значит любую из 14 можем выбрать =14вариантов;
теперь делаем группу тройку,
на каждую пару мальчиков одна девочка из 15, значит
ответ выбрать группу 3человека из два мальчика и одна девочка.
Г)) 2 девочки выбираем из 14 (одна болеет, не считаем); и 1 мальчик из 13;
Девочек первую выбрать вторую
1)) 14•13=182; но каждую девочку мы посчитали два раза АВ и ВА одинаково, поменяно местами. Значит делим на 2.
выбрать две девочки.
Мальчик 1 из 13, значит любого из всех и выбираем троих девочек и мальчика умножаем,
ответ: группу 2 девочки и один мальчик можно выбрать