ДАНО y = 1/x + 4x² ИССЛЕДОВАНИЕ. 1. Область определения.x ≠ 0,Х∈(-∞;0)∪(0;+∞) 2. Вертикальная асимптота: Х= 0. 3. Пересечение с осью Х. x = - 1/2*∛2 - (без комментов) 4. Пересечение с осью У. - нет. 5. Проверка на чётность. Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x) Функция ни четная ни нечетная.
6. Поведение в точке разрыва. lim(->0-) Y(x) = -∞. lim(->1+) Y(x) = +∞.
Горизонтальной асимптоты - нет.
8, Первая производная.
8*x³ = 1 и х= 1/2
6. Локальные экстремумы.
Y'(x) = 0 -при х= 1/2 Максимума - нет. Минимум -y(1/2) = 3. 7. Участки монотонности функции. Возрастает Х∈(1/2;+∞). Убывает на всех других интервалах. 8. Вторая производная -находим точки перегиба. Корень производной - f = -1/2*√3 ≈ - 0.87 .
9. Выпуклая - "горка" - Х∈[-0.87;0]
Вогнутая - "ложка" - Х∈(-∞;-0.87)∪(0;+∞) 10. График в приложении
При большом уменьшении - "почти" квадратная парабола.
y = 1/x + 4x²
ИССЛЕДОВАНИЕ.
1. Область определения.x ≠ 0,Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 0.
3. Пересечение с осью Х.
x = - 1/2*∛2 - (без комментов)
4. Пересечение с осью У. - нет.
5. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
6. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->1+) Y(x) = +∞.
Горизонтальной асимптоты - нет.
8, Первая производная.
8*x³ = 1 и х= 1/2
6. Локальные экстремумы.
Y'(x) = 0 -при х= 1/2
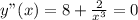
Максимума - нет. Минимум -y(1/2) = 3.
7. Участки монотонности функции.
Возрастает Х∈(1/2;+∞). Убывает на всех других интервалах.
8. Вторая производная -находим точки перегиба.
Корень производной - f = -1/2*√3 ≈ - 0.87 .
9. Выпуклая - "горка" - Х∈[-0.87;0]
Вогнутая - "ложка" - Х∈(-∞;-0.87)∪(0;+∞)
10. График в приложении
При большом уменьшении - "почти" квадратная парабола.
ПОЧТИ.Красота, а не график.