II рівень В групі спортсменів 15 курсантів з першого, 10 курсантів з другого і
5 - третього факультетів. Ймовірність виконання кваліфікаційної
норми такі: курсант першого 0,87, курсант другого - 0,76 і
курсант третього факультету - 0,74. Визначити ймовірність того, що
навмання взятий спортсмен виконає кваліфікаційну норму.
-
500
вероятность того, что наугад взятый спортсмен выполнит квалификационную норму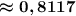
Пошаговое объяснение:
Уравнение полной вероятности.
Всего курсантов (15+10+5) = 30
Гипотезы и их вероятности (вероятности вычисляем по классическому определению вероятности P=m/n)
Н₁ = {выбран курсант 1 факультета}
P(H₁) = 15/30
Н₂ = {выбран курсант 2 факультета}
P(H₂) = 10/30
Н₃ = {выбран курсант 3 факультета}
P(H₃) = 5/30
Событие А = {наугад взятый спортсмен выполнит rвалификационную норму }
Условные вероятности нам даны в описании задачи
P(A|H₁) = 0,87
P(A|H₂) = 0,76
P(A|H₃) = 0,74
Формула полной вероятности
P(A) = P(H₁)*P(A|H₁) + P(H₂)*P(A|H₂) + P(H₃)*P(A|H₃)
Подставим наши данные
Таким образом, вероятность того, что наугад взятый спортсмен выполнит квалификационную норму ≈ 0,8117