Игральную кость бросают дважды найдите вероятность события при первом броске выпало чётное число очков, а при втором выпало не менее пяти очков. ответ округлите до тысячных
При первом броске, количество благоприятных нам случаев = 3
Так как нам нужны числа 2 4 6, а все числа это: 1 2 3 4 5 6
По этому по формуле вероятности (P(a)=, где m- кол-во благоприятных случаев, а n - общее количество всех возможных случаев):
В первом случае шанс - 0,5
Во втором случае нам подходят только 5 и 6, по этому шанс 2/6 = 1/3 ≈ 0,3333...
По правилам теории вероятности если нам нужны 2 независимых события то есть И в первый раз выпало чётное И во второй не меньше пяти, то вероятность что произойдет и то и то - произведение вероятностей.
0,5 * 0,333 ≈ 0,167
Если бы у нас было ИЛИ то ИЛИ то, то надо суммировать эти 2 шанса. Удачи.
Приблизительно 0,167
Пошаговое объяснение:
При первом броске, количество благоприятных нам случаев = 3
Так как нам нужны числа 2 4 6, а все числа это: 1 2 3 4 5 6
По этому по формуле вероятности (P(a)=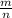 , где m- кол-во благоприятных случаев, а n - общее количество всех возможных случаев):
, где m- кол-во благоприятных случаев, а n - общее количество всех возможных случаев):
В первом случае шанс - 0,5
Во втором случае нам подходят только 5 и 6, по этому шанс 2/6 = 1/3 ≈ 0,3333...
По правилам теории вероятности если нам нужны 2 независимых события то есть И в первый раз выпало чётное И во второй не меньше пяти, то вероятность что произойдет и то и то - произведение вероятностей.
0,5 * 0,333 ≈ 0,167
Если бы у нас было ИЛИ то ИЛИ то, то надо суммировать эти 2 шанса. Удачи.