65
Пошаговое объяснение:
(10m+n)*m*n=1950
Число 1950 оканчивается на 0. Проверим, может ли 10m+n=10 или m*n=10.
m*n может равняться 10 только если m=10 и n=1 или n=10 и m=1, что противоречит условию (оба числа однозначные, образуют двузначное 10m+n).
10m+n также не может равняться 10, с учетом того что оба числа однозначные.
Если 10m+n10 и m*n10, а 1950 оканчивается на 0, значит n равно 5.
(10m+5)*5m=1950
5(2m+1)*5m=1950
(2m+1)*25m=1950
(2m+1)*m=78
2m^2+m-78=0
Решаем квадратное уравнение.
D=625
Квадратный корень из D равен 25
m1=(-1+25)/4=6
m2=(-1-25)/4=-6,5
-6,5 - не однозначное число, что противоречит условию.
Значит m=6, n=5
Проверяем:
65*6*5=1590
65
Пошаговое объяснение:
(10m+n)*m*n=1950
Число 1950 оканчивается на 0. Проверим, может ли 10m+n=10 или m*n=10.
m*n может равняться 10 только если m=10 и n=1 или n=10 и m=1, что противоречит условию (оба числа однозначные, образуют двузначное 10m+n).
10m+n также не может равняться 10, с учетом того что оба числа однозначные.
Если 10m+n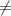 10 и m*n
10 и m*n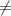 10, а 1950 оканчивается на 0, значит n равно 5.
10, а 1950 оканчивается на 0, значит n равно 5.
(10m+5)*5m=1950
5(2m+1)*5m=1950
(2m+1)*25m=1950
(2m+1)*m=78
2m^2+m-78=0
Решаем квадратное уравнение.
D=625
Квадратный корень из D равен 25
m1=(-1+25)/4=6
m2=(-1-25)/4=-6,5
-6,5 - не однозначное число, что противоречит условию.
Значит m=6, n=5
Проверяем:
65*6*5=1590