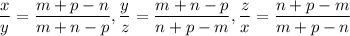1. Два велосипедиста проехали путь между A и B с постоянной скоростью, оба стартовали одновременно. Встретились в первый раз на расстоянии 11 км от пункта А (точка С).
Пусть весь путь от А до В равен S км.
Тогда первый велосипедист проехал 11 км, а второй (S - 11) км.
Пусть время велосипедистов до первой встречи равно t₁.
Выразим скорость:
2. Через некоторое время на обратном пути для обоих велосипедистов они встретились во второй раз на расстоянии 6 км от B.
То есть, первый и второй велосипедисты тронулись из пункта С, доехали соответственно до пунктов В и А, повернули назад и встретились в пункте Е.
Первый велосипедист проехал до пункта В расстояние (S-11) км и до пункта Е еще 6 км. Всего:
S - 11 + 6 = (S - 5) (км)
Второй до пункта А проехал 11 км и еще (S - 6) км до пункта Е.
Введём следующие обозначения. Обозначим вершины треугольника как A, B, C, причём AB : BC : AC = m : n : p. Обозначим точки касания с AB как M, с BC — N, AC — P, отрезки касательных AM = AP = x, BM = BN = y, CN = CP = z (отрезки касательных, проведённых из одной точки, равны).
Из отношения AB : BC : AC = m : n : p следует, что AB = mk, BC = nk, AC = pk. Тогда получаем
Вычтем из третьего уравнения второе и запишем его в системе с первым:
Подставим найденный x в третье уравнение и выразим z: .
Расстояние между A и B равно 27 км.
Пошаговое объяснение:
Требуется найти расстояние от А до В.
Вспомним формулы:
1. Два велосипедиста проехали путь между A и B с постоянной скоростью, оба стартовали одновременно. Встретились в первый раз на расстоянии 11 км от пункта А (точка С).
Пусть весь путь от А до В равен S км.
Тогда первый велосипедист проехал 11 км, а второй (S - 11) км.
Пусть время велосипедистов до первой встречи равно t₁.
Выразим скорость:
2. Через некоторое время на обратном пути для обоих велосипедистов они встретились во второй раз на расстоянии 6 км от B.
То есть, первый и второй велосипедисты тронулись из пункта С, доехали соответственно до пунктов В и А, повернули назад и встретились в пункте Е.
Первый велосипедист проехал до пункта В расстояние (S-11) км и до пункта Е еще 6 км. Всего:
S - 11 + 6 = (S - 5) (км)
Второй до пункта А проехал 11 км и еще (S - 6) км до пункта Е.
Всего:
11 + S - 6 = (S + 5) (км)
Пусть на это они затратили время t₂.
Тогда t₂:
Расстояние нулем быть не может ⇒ S = 27 км.
Расстояние между A и B равно 27 км.
Пошаговое объяснение:
Введём следующие обозначения. Обозначим вершины треугольника как A, B, C, причём AB : BC : AC = m : n : p. Обозначим точки касания с AB как M, с BC — N, AC — P, отрезки касательных AM = AP = x, BM = BN = y, CN = CP = z (отрезки касательных, проведённых из одной точки, равны).
Из отношения AB : BC : AC = m : n : p следует, что AB = mk, BC = nk, AC = pk. Тогда получаем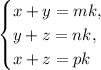
Вычтем из третьего уравнения второе и запишем его в системе с первым: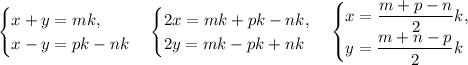
Подставим найденный x в третье уравнение и выразим z: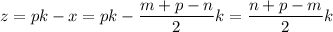 .
.
Тогда искомые отношения: