ДОМАШНЕЕ ЗАДАНИТЕ Реши задачу разными . 10. В городской школе в каждом клас- се обучаются 25 человек. Сколько человек обучается в одиннадцати- летней школе, если в каждой парал- лели по 3 класса («А», «Б», и «В»)? краткое условие
Разобьем прямую на отрезки длины 1 целыми числами (по сути, возьмем числовую ось). Обозначим это множество A.
Т.к. расстояние между любыми двумя точками множества М на прямой больше единицы, то каждый отрезок содержит не более одной точки множества М. Пусть множество - множество отрезков, содержащих точку множества М.
Поставим каждому отрезку в соответствие число, являющееся его левым концом. Тогда множество A счетно. А значит любое его подмножество счетно. Значит B счетно.
Поставим в соответствие каждой точке множества M отрезок из B, содержащий эту точку. Тогда между M и B есть биекция, а тогда М не более, чем счетное.
Для наглядности на листочке все пометил цифрами, смотри за вычислениями туда :)
1) Итак, для начала мы переведем время, за которая лодка может пройти туда-обратно в часы. Для этого составим дробь: в целых - целые часы, числитель - данные минуты, знаменатель - 60 (минут в одном часе).
2) Далее, возьмем за х собственную скорость лодки и составим табличку. Советую для таких типовых задач составлять такую таблицу, все становится понятнее. Колонки обозначаем как v - скорость, t - время, s - расстояние. Нам неизвестно расстояние, формула для него: s = vt. Заполняем табличку: скорость лодки по течению: x+1,5. Скорость лодки против течения: х-1,5. Время дано по условию: вписываем то, что мы перевели (в часах). Расстояние лодка проходит одинаковое что туда, что обратно.
Далее по внесенным данным составляем уравнение находим расстояние по течению и после течения путем умножения (s=vt) и приравниваем т.к. помним, что расстояние было одинаковым. Путем несложных вычислений находим х = 1,5
3) Находим расстояние между городами: в любую из частей уравнения подставляем найденный х = 1,5. Я подставил в первую. Тогда расстояние у нас равно 13.
Разобьем прямую на отрезки длины 1 целыми числами (по сути, возьмем числовую ось). Обозначим это множество A.
Т.к. расстояние между любыми двумя точками множества М на прямой больше единицы, то каждый отрезок содержит не более одной точки множества М. Пусть множество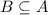
- множество отрезков, содержащих точку множества М.
Поставим каждому отрезку в соответствие число, являющееся его левым концом. Тогда множество A счетно. А значит любое его подмножество счетно. Значит B счетно.
Поставим в соответствие каждой точке множества M отрезок из B, содержащий эту точку. Тогда между M и B есть биекция, а тогда М не более, чем счетное.
собственная скорость лодки = 1,5 км/ч
расстояние между городами = 13
Пошаговое объяснение:
Для наглядности на листочке все пометил цифрами, смотри за вычислениями туда :)
1) Итак, для начала мы переведем время, за которая лодка может пройти туда-обратно в часы. Для этого составим дробь: в целых - целые часы, числитель - данные минуты, знаменатель - 60 (минут в одном часе).
2) Далее, возьмем за х собственную скорость лодки и составим табличку. Советую для таких типовых задач составлять такую таблицу, все становится понятнее. Колонки обозначаем как v - скорость, t - время, s - расстояние. Нам неизвестно расстояние, формула для него: s = vt. Заполняем табличку: скорость лодки по течению: x+1,5. Скорость лодки против течения: х-1,5. Время дано по условию: вписываем то, что мы перевели (в часах). Расстояние лодка проходит одинаковое что туда, что обратно.
Далее по внесенным данным составляем уравнение находим расстояние по течению и после течения путем умножения (s=vt) и приравниваем т.к. помним, что расстояние было одинаковым. Путем несложных вычислений находим х = 1,5
3) Находим расстояние между городами: в любую из частей уравнения подставляем найденный х = 1,5. Я подставил в первую. Тогда расстояние у нас равно 13.