Долго задача. Придумайте проект и рассчитайте сумму денег
необходимую для его реализации

Показать ответ

Ответ:

Георгий161

09.04.2023 11:28

Потому, что арабы заимствовали их у индусов! --)))
Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел.

Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, при к арабскому письму [1].

Индийскую систему записи широко популяризировал учёный Абу Джафар Мухаммад ибн Муса Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». Аль-Хорезми написал книгу «Об индийском счёте популяризации десятичной позиционной системы записи чисел во всём Халифате, вплоть до Мусульманской Испании. Вигиланский кодекс содержит первое упоминание и изображение арабских цифр (кроме нуля) в Западной Европе [2]. Они появились через мавров в Испании около 900 года.

Арабские цифры стали известны европейцам в X веке. Благодаря тесным связям христианской Барселоны (Барселонское графство) и мусульманской Кóрдовы (Кордовский халифат), Сильвестр II (папа римский с 999 по 1003 годы) имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности, он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления по сравнению с римскими цифрами и начал пропагандировать их внедрение в европейскую науку. В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении индо-арабских цифр.

0,0(0 оценок)

Ответ:

ak9512

25.05.2023 22:28

Пошаговое объяснение:

Первообразная функции - это такое выражение, производная которого равна исходной функции.

f(x)=2x+3;

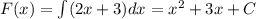
Первообразная: $F(x)=\int(2x+3)dx=x^2+3x+C$

Подставим координаты точки М в общий вид первообразной.

$2=1^2+3\cdot1+C\\ C=-2$

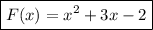
Искомая первообразная: $\boxed{F(x)=x^2+3x-2}$

f(x)=3x^2-2;

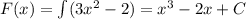
Первообразная: $F(x)=\int(3x^2-2)=x^3-2x+C$

Подставим координаты точки М в общий вид первообразной.

$4=2^3-2\cdot2+C\\ C=0$

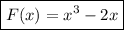
Искомая первообразная: $\boxed{F(x)=x^3-2x}$

$f(x)=1+\sin x;$

Первообразная: $F(x)=\int(1+\sin x)dx=x-\cos x+C$

Подставим координаты точки М в общий вид первообразной.

$1=0-\cos0+C\\ C=2$

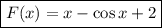
Искомая первообразная: $\boxed{F(x)=x-\cos x+2}$

$f(x)=3\cos x-2;$

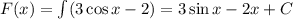
Первообразная: $F(x)=\int(3\cos x-2)=3\sin x-2x+C$

Подставим координаты точки М в общий вид первообразной.

$-1=3\sin\frac{\pi}{2}-2\cdot\frac{\pi}{2}+C\\ C=-4+\pi$

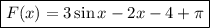
Искомая первообразная: $\boxed{F(x)=3\sin x-2x-4+\pi}$

$f(x)=\dfrac{1}{\sin^2(\frac{\pi}{2}+x)}=\dfrac{1}{\cos^2 x}$

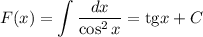
Первообразная: $F(x)=\displaystyle \int\dfrac{dx}{\cos^2 x}={\rm tg}x+C$

Подставим координаты точки М в общий вид первообразной.

$-1={\rm tg}(-\frac{\pi}{4})+C\\ -1=-1+C\\ C=0$

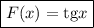
Искомая первообразная: $\boxed{F(x)={\rm tg}x}$

$f(x)=\dfrac{1}{\cos^2(\frac{3\pi}{2}-x)}=\dfrac{1}{\sin^2 x}$

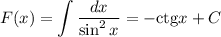
Первообразная: $F(x)=\displaystyle \int \dfrac{dx}{\sin^2 x}=-{\rm ctg}x+C$

Подставим координаты точки М в общий вид первообразной.

$\sqrt{3}={\rm ctg}\frac{5\pi}{6}+C\\ \sqrt{3}=-\sqrt{3}+C\\ C=2\sqrt{3}$

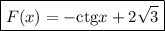
Искомая первообразная: $\boxed{F(x)=-{\rm ctg}x+2\sqrt{3}}$

f(x)=(x-1)^3

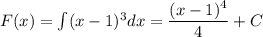
Общий вид первообразной: $F(x)=\int(x-1)^3dx=\dfrac{(x-1)^4}{4}+C\\$

f(x)=(1-2x)^2=1-4x+4x^2

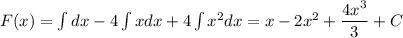
Общий вид первообразной: $F(x)=\int dx-4\int xdx+4\int x^2dx=x-2x^2+\dfrac{4x^3}{3}+C\\$

$f(x)=\dfrac{1}{2\sqrt{x}}+11x^{10}$

Общий вид первообразной: $F(x)=\sqrt{x}+11\cdot \dfrac{x^{11}}{11}+C=\sqrt{x}+x^{11}+C$

$f(x)=\dfrac{1}{x^2}+12x^8$

Общий вид первообразной: $F(x)=\displaystyle \int\bigg(\dfrac{1}{x^2}+12x^8\bigg)dx=-\dfrac{1}{x}+12\cdot \dfrac{x^9}{9}+C=-\dfrac{1}{x}+\dfrac{4x^9}{3}+C$