Разобьем прямую на отрезки длины 1 целыми числами (по сути, возьмем числовую ось). Обозначим это множество A.
Т.к. расстояние между любыми двумя точками множества М на прямой больше единицы, то каждый отрезок содержит не более одной точки множества М. Пусть множество - множество отрезков, содержащих точку множества М.
Поставим каждому отрезку в соответствие число, являющееся его левым концом. Тогда множество A счетно. А значит любое его подмножество счетно. Значит B счетно.
Поставим в соответствие каждой точке множества M отрезок из B, содержащий эту точку. Тогда между M и B есть биекция, а тогда М не более, чем счетное.
Разобьем прямую на отрезки длины 1 целыми числами (по сути, возьмем числовую ось). Обозначим это множество A.
Т.к. расстояние между любыми двумя точками множества М на прямой больше единицы, то каждый отрезок содержит не более одной точки множества М. Пусть множество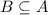 - множество отрезков, содержащих точку множества М.
- множество отрезков, содержащих точку множества М.
Поставим каждому отрезку в соответствие число, являющееся его левым концом. Тогда множество A счетно. А значит любое его подмножество счетно. Значит B счетно.
Поставим в соответствие каждой точке множества M отрезок из B, содержащий эту точку. Тогда между M и B есть биекция, а тогда М не более, чем счетное.