Пусть последовательность такова, что для всех выполнено неравенство . Тогда верно неравенство . Это легко видеть, заменяя члены с использованием неравенства.
В нашем случае , неравенство верно для всех натуральных . Значит, искомая сумма не превосходит . Для очевидно.
Пусть последовательность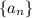 такова, что для всех
такова, что для всех  выполнено неравенство
выполнено неравенство 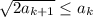 . Тогда верно неравенство
. Тогда верно неравенство 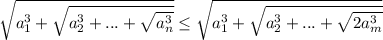 . Это легко видеть, заменяя члены с использованием неравенства.
. Это легко видеть, заменяя члены с использованием неравенства.
В нашем случае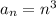 , неравенство
, неравенство 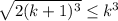 верно для всех натуральных
верно для всех натуральных 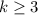 . Значит, искомая сумма не превосходит
. Значит, искомая сумма не превосходит 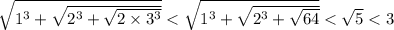 . Для
. Для 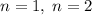 очевидно.
очевидно.