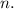Докажем методом математической индукции.
1) При выполнено .
2) Предположим, что при выражение
3) Докажем теперь при
Первая скобка делится на 16 по предположению 2), а слагаемое очевидно делится на 16, следовательно и сумма этих слагаемых делится на 16. Следовательно, выражение для любых натуральных
Докажем методом математической индукции.
1) При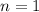 выполнено
выполнено  .
.
2) Предположим, что при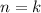 выражение
выражение 
3) Докажем теперь при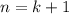
Первая скобка делится на 16 по предположению 2), а слагаемое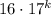 очевидно делится на 16, следовательно и сумма этих слагаемых делится на 16. Следовательно, выражение
очевидно делится на 16, следовательно и сумма этих слагаемых делится на 16. Следовательно, выражение 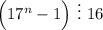 для любых натуральных
для любых натуральных