Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
228GGnyb
26.10.2020 09:53 •
Математика
До іть,будь ласка,з роботою по вищій математиці. Знайти похідну
Показать ответ
Ответ:
turkeev90
16.12.2022 06:00
1.
2.
Пошаговое объяснение:
Найти производную:
1.
2.
Производная суммы равна сумме производных.Формула:
1. Преобразуем данное выражение:
Производная равна:
Производная произведения:
;
2.
Производная равна:
0,0
(0 оценок)
Популярные вопросы: Математика
ccfnwj3662
14.09.2022 07:46
Нарисуй прямоугольник, площадь которого 18 см², а длина одной из сторон 6 см. Найди периметр этого прямоугольника. Проведи отрезок, чтобы получился квадрат. Найди периметр...
Aika2216
17.08.2022 07:33
Перенесіть у ліву частину рівняння всі доданки, що містять невідоме, а у праву - усі доданки, що не містять невідомого: 4х - 5 = 2х + 34х - 2х = 5 + 32х - 5 = 4х + 34х...
ролл10
03.09.2021 07:44
Отрезок ab разделяется точкой c(0,8; 2,6) в отношении 2:3...
Updatek
15.02.2023 16:23
1% этого числа составляет 700 7% этого числа равны 9,8350% этого числа равны 71% этого числа равен 5 1/21/8% этого числаравен 1,2525% этого числа равны 4% от 25...
lera08862
19.08.2020 13:17
В треугольнике АВС ВС=34см. Из середины отрезка ВС к прямой АС проведён перпендикуляр который делит сторону АС на отрезки АF=25 и FC=15см. Найдите площадь треугольника...
crystall5555
06.12.2020 15:52
5. Даны точки К(-9) и М(-1). a) Найдите координату точки Ь, противоположную координата точки К. Ь) Изобразите точки К, М и [‚ на координатном луче. с) Найдите расстоянше...
Лідія200445
14.01.2022 18:10
9м3=дм3 18000дм3=???м3 3000см3=???дм3 60000см3=???дм3...
lybchikfreed
23.05.2022 17:40
4. Запишите в виде несократимой дроби: a) 147/189 b) 900/1075...
gjhjcznrj
04.05.2021 13:34
Көмек достар плс плс плс плс плс...
veronikamarina20062
04.05.2021 13:34
ответ давать цифра примера и ответ...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
1.![\displaystyle y'=\frac{12}{5\sqrt[5]{x^2} } +\frac{12}{x^3} -\frac{1}{\sqrt{x} } +2](/tpl/images/5104/4590/5259a.png)
2.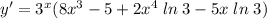
Пошаговое объяснение:
Найти производную:
1.![\displaystyle y=4\sqrt[5]{x^3}-\frac{6x+2\sqrt{x^7} }{x^3} +2x-3](/tpl/images/5104/4590/7df9d.png)
2.
Производная суммы равна сумме производных.Формула:1. Преобразуем данное выражение:
Производная равна:
![\displaystyle y'=4\cdot \frac{3}{5}x^{-\frac{2}{5} } -6\cdot (-2)x^{-3}-2\cdot \frac{1}{2}x^{-\frac{1}{2} }+2-0=\\ \\=\frac{12}{5\sqrt[5]{x^2} } +\frac{12}{x^3} -\frac{1}{\sqrt{x} } +2](/tpl/images/5104/4590/a986d.png)
Производная произведения:2.
Производная равна: