Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от до , либо от до .
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
, делящееся на 3
, делящееся на 4
, делящееся на 5
, делящееся на 6
, делящееся на 7
, делящееся на 8
Рассмотрим утверждение "" делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит делится на 4, делится на 4, делится на 4, делится на 2, значит - четное.
Рассмотрим утверждение "" делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, делится на 3, делится на 3. Выпишем пары цифр, где , а - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение "" делится на 7"". Если делится на 7, то делится на 7, делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
Пошаговое объяснение: а) мода - самое повторяющееся число в выборке, а это число 2, б) медиана - серединное число в выборке, при записании ряда в порядке возрастания, в) размах - разница между наибольшим и наименьшим числом выборки, г) средне квадратичное отклонение вычисляется как квадратный корень из дисперсии, которая в свою очередь считается по формуле:
S^2=(1/n-1)*∑(xi-X*)^2, где xi - каждое значение выборки, X* среднее значение, n количество значений. Тогда дисперсия = 1,5, а средне квадратичное отклонение 1,25
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от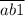 до
до 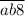 , либо от
, либо от 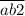 до
до 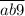 .
.
Значит, в любом случае среди этих чисел есть следующие:
Рассмотрим утверждение ""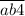 делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит
делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит 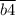 делится на 4,
делится на 4, 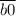 делится на 4,
делится на 4, 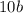 делится на 4,
делится на 4, 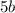 делится на 2, значит
делится на 2, значит 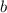 - четное.
- четное.
Рассмотрим утверждение ""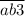 делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит,
делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, 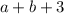 делится на 3,
делится на 3, 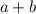 делится на 3. Выпишем пары цифр, где
делится на 3. Выпишем пары цифр, где 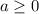 , а
, а 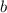 - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение ""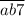 делится на 7"". Если
делится на 7"". Если 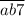 делится на 7, то
делится на 7, то 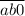 делится на 7,
делится на 7, 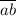 делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13
ответ: а)2, б)2, в)4, г)≈1,25
Пошаговое объяснение: а) мода - самое повторяющееся число в выборке, а это число 2, б) медиана - серединное число в выборке, при записании ряда в порядке возрастания, в) размах - разница между наибольшим и наименьшим числом выборки, г) средне квадратичное отклонение вычисляется как квадратный корень из дисперсии, которая в свою очередь считается по формуле:
S^2=(1/n-1)*∑(xi-X*)^2, где xi - каждое значение выборки, X* среднее значение, n количество значений. Тогда дисперсия = 1,5, а средне квадратичное отклонение 1,25