Даугава имеет длину 1005 км, а Вента короче на 659 км. Однако Гауя на 106 км длиннее Венты. Вычерчивая длину рек в километрах до целых сотен, напишите упрощенное выражение отказа для каждых двух длин реки!
Для начала запишем правила нахождения производных, U(x) и V(x) функции от переменной икс, тогда
1)(U(x)±V(x))'=U'(x)±V'(x) (производная суммы или разности двух или более функций равна сумме или разности их производных) больше переменную писать не буду, но под U V будем понимать именно функции от х
2)(U*V)'=U'V+V'U (производная произведения - сумма произведений каждой функции на каждую ее производную)
3) это производная частного, ну и последнее правило это производная сложной функции
4) K(y), y(x) K'x=y'x*x'. Т.е. сначала находим производную внешней функции и умножаем на производную внутренней
5) константу можно вынести за знак производной
Расписать всю таблицу нахождения производных, я конечно могу, но вы не представляете как это долго, посмотрите в учебнике)
итак,
10x^9+5x^4+1.
сократим на х в квадрате, и все хорошо
заметим, что 5 в квадрате это число, тогда
4x+1/2.
Теперь хитрый прием, представим 5 на корень из икс как 5 умножить на икс в степени минус 1/2 и найдем как производную от степенной, тогда 5 оставим, минус 1/2 вынесем, -1/2-1=-3/2. и вернем арифмитический корень, в итоге получим, 5 делить на 2 корня из икса в кубе
x^2sinx это произведение, тогда 2xsinx+x^2cosx=x(2sinx+xcosx) выносить икс не обязательно.
(1+sinx)^2= тут есть 2 пути, первый раскрыть квадрат суммы тогда
1+2sinx+sin^2x и производная от суммы 0+2cosx+ и вот теперь
синус квадрат икс это сложная функция, т.е. что-то в квадрате это внешняя функция, и непосредственно синус от икс это внутренняя, тогда 2sinx(степенная внешняя)*sinx'=2sinx*cosx=sin(2x). Второй вариант это расписать квадрат как sinx*sinx=cosx*sinx+sinx*cosx=2sinxcosx=sin(2x)
ну и второй вариант, это обозначить всю изначальную скобку за внутреннюю функцию, а ее квадрат за внешнюю, тогда получим
2(1+sinx)*(1+sinx)'=2(1+sinx)*cosx=(2+2sinx)cosx=2cosx+2sinxcosx=2cosx+sin(2x) как мы видим ответы совпадают. Мы вроде разобрали все правила и дальше вы можете решать по аналогии, но хочу сделать пару замечаний)
8)2а- это число, поэтому 1/2а можно сразу вынести, для синуса 3x это сложная функция и мы получим cos(3x)*3x'=3cos(3x)/2a
12) корень кубический лучше представить как вся эта разность в степени 1/3, а вот в 10-ом этого можно не делать
15) достаточно сложное произведение, но я в вас верю, если что, пишите
16) n-просто число, представьте как икс в степени 2/n
Пошаговое объяснение:
Для начала запишем правила нахождения производных, U(x) и V(x) функции от переменной икс, тогда
1)(U(x)±V(x))'=U'(x)±V'(x) (производная суммы или разности двух или более функций равна сумме или разности их производных) больше переменную писать не буду, но под U V будем понимать именно функции от х
2)(U*V)'=U'V+V'U (производная произведения - сумма произведений каждой функции на каждую ее производную)
3)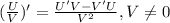 это производная частного, ну и последнее правило это производная сложной функции
это производная частного, ну и последнее правило это производная сложной функции
4) K(y), y(x) K'x=y'x*x'. Т.е. сначала находим производную внешней функции и умножаем на производную внутренней
5) константу можно вынести за знак производной
Расписать всю таблицу нахождения производных, я конечно могу, но вы не представляете как это долго, посмотрите в учебнике)
итак,
10x^9+5x^4+1.
заметим, что 5 в квадрате это число, тогда
4x+1/2.
Теперь хитрый прием, представим 5 на корень из икс как 5 умножить на икс в степени минус 1/2 и найдем как производную от степенной, тогда 5 оставим, минус 1/2 вынесем, -1/2-1=-3/2. и вернем арифмитический корень, в итоге получим, 5 делить на 2 корня из икса в кубе
x^2sinx это произведение, тогда 2xsinx+x^2cosx=x(2sinx+xcosx) выносить икс не обязательно.
(1+sinx)^2= тут есть 2 пути, первый раскрыть квадрат суммы тогда
1+2sinx+sin^2x и производная от суммы 0+2cosx+ и вот теперь
синус квадрат икс это сложная функция, т.е. что-то в квадрате это внешняя функция, и непосредственно синус от икс это внутренняя, тогда 2sinx(степенная внешняя)*sinx'=2sinx*cosx=sin(2x). Второй вариант это расписать квадрат как sinx*sinx=cosx*sinx+sinx*cosx=2sinxcosx=sin(2x)
ну и второй вариант, это обозначить всю изначальную скобку за внутреннюю функцию, а ее квадрат за внешнюю, тогда получим
2(1+sinx)*(1+sinx)'=2(1+sinx)*cosx=(2+2sinx)cosx=2cosx+2sinxcosx=2cosx+sin(2x) как мы видим ответы совпадают. Мы вроде разобрали все правила и дальше вы можете решать по аналогии, но хочу сделать пару замечаний)
8)2а- это число, поэтому 1/2а можно сразу вынести, для синуса 3x это сложная функция и мы получим cos(3x)*3x'=3cos(3x)/2a
12) корень кубический лучше представить как вся эта разность в степени 1/3, а вот в 10-ом этого можно не делать
15) достаточно сложное произведение, но я в вас верю, если что, пишите
16) n-просто число, представьте как икс в степени 2/n
Пошаговое объяснение:
1) Числа кратные 9 можно записать в виде 9n, где n - натуральное число:
9, 18, 27, 36, 45, 54 и т.д.
Подсчитаем количество чисел кратных 9 до 30. Их, как видно из ряда выше всего 3 - 9,18,27. Заметим, что целая часть числа 30/3 равна 3.
Очевидно, что это правило можно применить для любого числа.
Таким образом, количество чисел кратных 9 , содержащиеся среди чисел от 1 до 600, равно целой части 600/9 - 66
ответ: 66
2) Количество чисел кратных 3 , содержащиеся среди чисел от 1 до 600, равно целой части