1) Переводим единицы измерения
1 пуд = 40 фунтов
1 грн ≈ 3 рубля (точнее 1 грн = 2,6 руб.)
2)
10,5 пудов = 10,5 · 40 = 420 фунтов
3) 6 гривен = 6 · 3 = 18 рублей
4) 18 · 420 = 7560 (руб) - стоит весь кофе первого сорта.
5) 21 пуд = 21 · 40 = 840 фунтов
6) 12 · 21 = 252 (руб) - стоит весь кофе второго сорта.
7) 420 фунтов + 840 фунтов = 1260 фунтов - масса всей смеси
8) 7560 руб + 252 руб = 7812 руб. стоит вся смесь.
9) 7812 руб. : 1260 фунтов = 6,2 руб стоит 1 фунт смеси (в рублях).
10) 6,2 руб : 3 ≈ 2,06 (грн.) стоит 1 фунт смеси (в гривнах)
ответ: 6,2 руб или 2,06 грн
P.S. Соотношение гривны к рублю взято из расчета на сегодняшний день, возможно для этой задачи в учебнике указано другое соотношение, например,
1 грн = 4 руб
или 1 грн = 5 руб.
Дано:
- точки, принадлежащие плоскости П: О(0; 0; 0), М(0; 2; –2), N(2; 2; 2),
- плоскость yOz.
Находим векторы:
ОМ = (0; 2; –2), ОN (2; 2; 2).
Нормальный вектор n плоскости П равен векторному произведение векторов ОМ и ОN.
i j k| i j
0 2 -2| 0| 2
2 2 2| 2 2 = 4i - 4j + 0k - 0j + 4i - 4k = 8i - 4j - 4k.
n = (8; -4; -4).
У координатной плоскости yOz нормальным вектором является координатный вектор k=(1; 0; 0).
Находим косинус угла α между нормальными векторами плоскостей П и плоскостью yOz это и будет угол между заданными плоскостями.
Сначала надо определить модули векторов:
|n| = √(8² + (-4)² + (-4)²) = √(64 + 16 +16) = √96 = 4√6.
|k| = 1.
cos α = (8*1 + -4*0 + -4*0)/(4√6*1) = 8/4√6 = 2/√6 = √(2/3).
α = arc cos(√(2/3)) = 0,61548 радиан или 35,26439 градуса.
1) Переводим единицы измерения
1 пуд = 40 фунтов
1 грн ≈ 3 рубля (точнее 1 грн = 2,6 руб.)
2)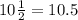
10,5 пудов = 10,5 · 40 = 420 фунтов
3) 6 гривен = 6 · 3 = 18 рублей
4) 18 · 420 = 7560 (руб) - стоит весь кофе первого сорта.
5) 21 пуд = 21 · 40 = 840 фунтов
6) 12 · 21 = 252 (руб) - стоит весь кофе второго сорта.
7) 420 фунтов + 840 фунтов = 1260 фунтов - масса всей смеси
8) 7560 руб + 252 руб = 7812 руб. стоит вся смесь.
9) 7812 руб. : 1260 фунтов = 6,2 руб стоит 1 фунт смеси (в рублях).
10) 6,2 руб : 3 ≈ 2,06 (грн.) стоит 1 фунт смеси (в гривнах)
ответ: 6,2 руб или 2,06 грн
P.S. Соотношение гривны к рублю взято из расчета на сегодняшний день, возможно для этой задачи в учебнике указано другое соотношение, например,
1 грн = 4 руб
или 1 грн = 5 руб.
Дано:
- точки, принадлежащие плоскости П: О(0; 0; 0), М(0; 2; –2), N(2; 2; 2),
- плоскость yOz.
Находим векторы:
ОМ = (0; 2; –2), ОN (2; 2; 2).
Нормальный вектор n плоскости П равен векторному произведение векторов ОМ и ОN.
i j k| i j
0 2 -2| 0| 2
2 2 2| 2 2 = 4i - 4j + 0k - 0j + 4i - 4k = 8i - 4j - 4k.
n = (8; -4; -4).
У координатной плоскости yOz нормальным вектором является координатный вектор k=(1; 0; 0).
Находим косинус угла α между нормальными векторами плоскостей П и плоскостью yOz это и будет угол между заданными плоскостями.
Сначала надо определить модули векторов:
|n| = √(8² + (-4)² + (-4)²) = √(64 + 16 +16) = √96 = 4√6.
|k| = 1.
cos α = (8*1 + -4*0 + -4*0)/(4√6*1) = 8/4√6 = 2/√6 = √(2/3).
α = arc cos(√(2/3)) = 0,61548 радиан или 35,26439 градуса.