Дано положительное число a. известно, что уравнение - вопрос №319584691 от jeniainna 24.11.2020 16:14

Question

Математика: Дано положительное число a. известно, что уравнение x3+1=ax имеет ровно два положительных корня, и отношение большего из них к меньшему равно 2018. уравнение x3+1=ax2 также имеет ровно два положительных корня. докажите, что отношение большего из них к меньшему также равно 2018.

jeniainna · Answer

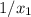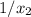Обозначим положительные корни второго уравнения как 1/x_1 и 1/x_2 . Так как сами корни положительны, то и 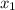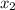x_1 , x_2 тоже положительны и не равны.

Подставим эти корни во второе уравнение, получатся уравнения вида

$\left(\dfrac1{x_i}\right)^3+1=a\left(\dfrac 1{x_i}\right)^2$

Умножим это уравнение на положительное число вида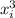 x_i^3 , получим первое уравнение:

1+x_i^3=ax_i

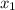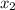Поскольку x_1 и x_2 - положительные неравные числа, то они и являются корнями первого уравнения. По условию, отношение большего к меньшему равно 2018, пусть для определённости 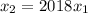x_2=2018x_1 . Тогда отношение корней второго уравнения равно

$\dfrac{1/x_1}{1/x_2}=\dfrac{x_2}{x_1}=2018$

P.S. на самом деле, из условия можно определить значение a. Оно оказывается равным

$\dfrac{4074343}{\sqrt[3]{4074342^2}}$