1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∠A = ∠C ;
2. так как проведена биссектриса, то ∠ABD = ∠CBD ;
3. стороны AB = CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — равнобедренный.
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит равны все соответствующие элементы, в том числе стороны AD = CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
AD = 34 см
Рассмотрим треугольники ΔABD и Δ BCD
(треугольник записать в алфавитном порядке).
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∠A = ∠C ;
2. так как проведена биссектриса, то ∠ABD = ∠CBD ;
3. стороны AB = CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — равнобедренный.
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит равны все соответствующие элементы, в том числе стороны AD = CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.
AD = АС/2 = 68/2 = 34 см
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую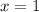 (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
(см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
А теперь складываем и находим искомую площадь.
ответ: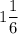 .
.