Дана правельная четырехугольная пирамида. Обозначим: а - сторона основания, l - апофема, P - периметр основания, Aб - площадь боковой поверхности, A - площадь полной поверхности. найдите:
а)P,Aб,А, если а=6м,l=12м
в)а,Р,А, если l=16м, Аб=288м^2
д)а,к,Р, если Аб=352м^2,А=416м^2
2001 ^ 2001 = 1
24 ^ 21 = 4
9 ^ 20 - 7 ^ 20 = 0
8 ^ 99 = 2
3 ^ 101 = 3
549 ^ 49 = 9
2 ^ 2015 = 8
1993 ^ 1993 = 9
777 ^ 333 + 333 ^ 777 = 0
Пошаговое объяснение:
2001 ^ 2001 = 1
т.к. 1 в любой степени оканчивается 1, т.к. 1 * 1 = 1 - только один вариант последней цифры
24 ^ 21 = 4
т.к. 4 в любой степени оканчивается только на 4 и на 6, при этом нечётная степень - на 4, а чётная - на 6 оканчивается, у нас 21 - нечётное число, выбираем именно 4 на конце
9 ^ 20 - 7 ^ 20 = 0 (1 - 1 = 0)
т.к. 9 в любой степени оканчивается только на 9 и на 1, при этом нечётная степень - на 9, а чётная - на 1 оканчивается, у нас 20 - чётное число, выбираем именно 1 на конце
т.к. 7 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 7, на 9, на 3 и на 1, при этом период выбора - четыре цифры, в показателе степени 20 помещается целых пять периодов по четыре цифры, выбираем четвёртый вариант цифры окончания (на 7, 9, 3, 1) - именно 1 на конце
и, наконец, при вычитании этих двух многозначных чисел, оканчивающихся на 1, имеем 1 - 1 = 0 в конце
Аналогично рассуждаем:
8 ^ 99 = 2
т.к. 8 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 8, на 4, на 2 и на 6, при этом период выбора - четыре цифры, в показателе степени 99 помещается после целых периодов ещё три цифры, выбираем третий вариант цифры окончания (на 8, 4, 2, 6) - именно 2 на конце
3 ^ 101 = 3
т.к. 3 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 3, на 9, на 7 и на 1, при этом период выбора - четыре цифры, в показателе степени 101 помещается после 25 целых периодов по четыре цифры ещё одна цифра, выбираем первый вариант цифры окончания (на 3, на 9, на 7 и на 1) - именно 3 на конце
549 ^ 49 = 9
т.к. 9 в любой степени оканчивается только на 9 и на 1, при этом нечётная степень - на 9, а чётная - на 1 оканчивается, у нас 49 - нечётное число, выбираем именно 9 на конце
2 ^ 2015 = 8
т.к. 2 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 2, на 4, на 8 и на 6, при этом период выбора - четыре цифры, в показателе степени 2015 помещается после целых периодов по четыре цифры ещё три цифры, выбираем третий вариант цифры окончания (на 2, на 4, на 8 и на 6) - именно 8 на конце
1993 ^ 1993 = 9
т.к. 3 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 3, на 9, на 7 и на 1, при этом период выбора - четыре цифры, в показателе степени 1993 помещается после целых периодов по четыре цифры ещё две цифры, выбираем второй вариант цифры окончания (на 3, на 9, на 7 и на 1) - именно 9 на конце
777 ^ 333 + 333 ^ 777 = 0 (7 + 3 = 0)
т.к. 7 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 7, на 9, на 3 и на 1, при этом период выбора - четыре цифры, в показателе степени 333 помещается после целых периодов по четыре цифры ещё одна цифра, выбираем первый вариант цифры окончания (на 7, на 9, на 3 и на 1) - именно 7 на конце
т.к. 3 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 3, на 9, на 7 и на 1, при этом период выбора - четыре цифры, в показателе степени 777 помещается после целых периодов по четыре цифры ещё одна цифра, выбираем первый вариант цифры окончания (на 3, на 9, на 7 и на 1) - именно 3 на конце
и, наконец, выполняем сложение двух многозначных чисел, одно оканчивается на 7, другое - на 3, тогда имеем: 7 + 3 = 10, т.е. оканчивается на 0.
Внимание, расшифровываю
Пошаговое объяснение:
Обозначим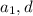
-- первый член арифметической прогрессии и разность арифметической прогрессии соответственно (то есть, разность между соседними элементами пусть равна 
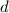). Тогда второй член последовательности равен
а седьмой равен
По условию мы знаем, что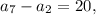
подставляя выражения для 
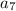и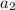 
получаем такое уравнение:
Итак, теперь разность мы знаем. Воспользуемся условием, что третий член равен 9:
с одной стороны
с другой
Значит
то есть
Пусть нам надо взять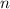
членов, чтобы получить сумму
По формуле, сумма арифметической прогрессии равна
Так как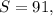
то нам надо решить квадратное уравнение
Решая это уравнение по формуле дискриминанта, получаем 2 решения: