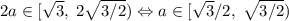1. Пусть , . Заметим, что и монотонно убывают, значит, функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения не более двух корней.
2. Заметим, что если является решением, то тоже. Очевидно, что является осью симметрии (причем единственной) графика . Иначе говоря, пара исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы . Итак, пробегает область значения рассматриваемой функции, кроме того , которому соответствует (это ).
3. Функция непрерывна, поэтому достаточно посмотреть на наименьшее и наибольшее значения. Наименьшее значение достигается в 0 (то есть значение , а наибольшее в . Получаем ответ:
Пошаговое объяснение:
Червей в грибе по условию задачи может быть: тощих - любое количество, обычных - не более 4.
Вычислим наименьшую долю тощих червей. Это будет в том случае, если обычных червей будет как можно больше (по 4 в грибе), а тощих - как можно меньше.
Грибы будут плохие и неплохие. Рассмотрим плохие грибы.
1. Плохие грибы. В нем живут от 12 червей: 8 тощих и 4 обычных - это дает наименьшую долю тощих.
2. Неплохие грибы. В нем живут не более 11 червей: 0 тощих и 4 обычных - это дает наименьшую долю тощих.
Итого:
если n плохих грибов и 3n неплохих, доля тощих червей равна:
(8n + 0) / (12n + 12n) = 8n/24n = 1/3.
1. Пусть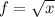 ,
, 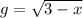 . Заметим, что
. Заметим, что 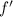 и
и 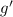 монотонно убывают, значит,
монотонно убывают, значит, 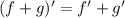 функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения
функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения 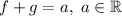 не более двух корней.
не более двух корней.
2. Заметим, что если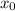 является решением, то
является решением, то  тоже. Очевидно, что
тоже. Очевидно, что 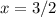 является осью симметрии (причем единственной) графика
является осью симметрии (причем единственной) графика 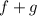 . Иначе говоря, пара
. Иначе говоря, пара 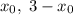 исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы
исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы 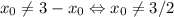 . Итак,
. Итак, 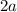 пробегает область значения рассматриваемой функции, кроме того
пробегает область значения рассматриваемой функции, кроме того  , которому соответствует
, которому соответствует 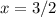 (это
(это 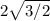 ).
).
3. Функция непрерывна, поэтому достаточно посмотреть на наименьшее и наибольшее значения. Наименьшее значение достигается в 0 (то есть значение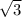 , а наибольшее в
, а наибольшее в 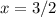 . Получаем ответ:
. Получаем ответ: