Сумма чисел: 2/5+5/8+11/25 Приводим к общему знаменателю, общий знаменатель у этих трех дробей равен 25*8=200 Приводим к общему знаменателю 200, для первой дроби доп множитель: 200:5=40, для второй 200:8=25 для третьей 200:25=8 В итоге получаем: (40+25+8)/200=72/200. Сокращаем на 8 получаем 9/25 это второе число Теперь произведение: 33 1/3 преобразуем в обыкновенную дробь и получаем (33*3+1)/3=100/3 Умножаем 9/25*100/3 Можно сократить 9 и 3 на 3 в числителе останется 3. А 100 и 25 сократить на 25 останется 4 в числителе. В итоге 3*4=12 ответ: 12
Имеем линейное неоднородное дифференциальное уравнение (ЛНДУ) с постоянными коэффициентами.
Общее решение этого уравнения:
— общее решение соответствующего однородного уравнения:
Воспользуемся методом Эйлера. Подстановка: .
Тогда получим характеристическое уравнение:
Имеем комплексно-сопряженные корни вида
Здесь и
Тогда и
Используем формулу Эйлера:
Значит,
Таким образом, фундаментальная система решений: — линейно независимые функции.
Общее решение:
— частное решение ЛНДУ с постоянными коэффициентами. Для его нахождения используется метод подбора вида частного решения по виду правой части уравнения.
Правая часть второго типа:
В нашем уравнении и не совпадает корнем однородного ЛДУ, а именно: и , поэтому , где — неизвестный коэффициент, который нужно найти.
Здесь и
Подставим и в заданное уравнение со специальной правой частью:
Частное решение:
Общее решение заданного дифференциального уравнения:
2/5+5/8+11/25
Приводим к общему знаменателю, общий знаменатель у этих трех дробей равен 25*8=200
Приводим к общему знаменателю 200, для первой дроби доп множитель: 200:5=40, для второй 200:8=25 для третьей 200:25=8 В итоге получаем:
(40+25+8)/200=72/200. Сокращаем на 8 получаем 9/25 это второе число
Теперь произведение:
33 1/3 преобразуем в обыкновенную дробь и получаем (33*3+1)/3=100/3
Умножаем 9/25*100/3 Можно сократить 9 и 3 на 3 в числителе останется 3. А 100 и 25 сократить на 25 останется 4 в числителе.
В итоге 3*4=12 ответ: 12
Имеем линейное неоднородное дифференциальное уравнение (ЛНДУ) с постоянными коэффициентами.
Общее решение этого уравнения:
Воспользуемся методом Эйлера. Подстановка: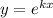 .
.
Тогда получим характеристическое уравнение:
Имеем комплексно-сопряженные корни вида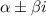
Здесь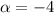 и
и 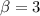
Тогда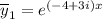 и
и 
Используем формулу Эйлера: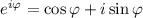
Значит,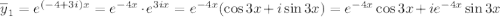
Таким образом, фундаментальная система решений: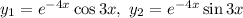 — линейно независимые функции.
— линейно независимые функции.
Общее решение: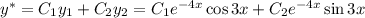
Правая часть второго типа: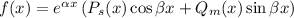
В нашем уравнении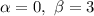 и не совпадает корнем однородного ЛДУ, а именно:
и не совпадает корнем однородного ЛДУ, а именно: 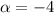 и
и 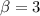 , поэтому
, поэтому  , где
, где 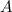 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Здесь и
и 
Подставим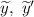 и
и 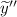 в заданное уравнение со специальной правой частью:
в заданное уравнение со специальной правой частью:
Частное решение:
Общее решение заданного дифференциального уравнения:
ответ: