Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение . Таким образом, синус от 60 градусов равен .
По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
Поскольку касательные перпендикулярны радиусу в точке касания, то треугольники ОАС и OBD прямоугольные. Рассмотрим их. Здесь:
- АО=ВО как радиусы окружности;
- <COA=<DOB как вертикальные углы.
Используем один из признаков равенства прямоугольных треугольников: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Значит, в равных треугольниках ОАС и OBD равны и их гипотенузы. ОС=OD.
sin (60°) = sin (π/3) = (√3)/2.
Пошаговое объяснение:
Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение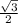
. Таким образом, синус от 60 градусов равен 
.
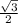По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
просто посмотреть значение в таблице.
Пошаговое объяснение:
Поскольку касательные перпендикулярны радиусу в точке касания, то треугольники ОАС и OBD прямоугольные. Рассмотрим их. Здесь:
- АО=ВО как радиусы окружности;
- <COA=<DOB как вертикальные углы.
Используем один из признаков равенства прямоугольных треугольников: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Значит, в равных треугольниках ОАС и OBD равны и их гипотенузы. ОС=OD.